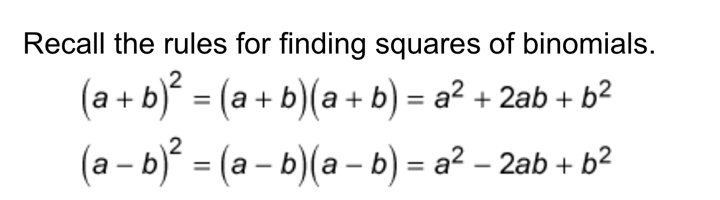Algebra 1 8-7 Guided Practice: Factoring Special Cases
By Matt Richardson
starstarstarstarstarstarstarstarstarstar
Last updated almost 3 years ago
16 Questions
10 points
10
Question 1
1.
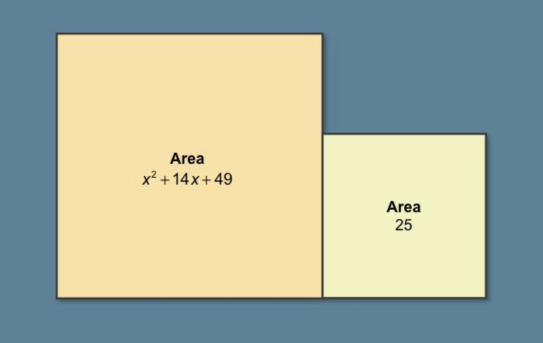
Solve It! The diagram shows two adjacent squares and their areas. In terms of x, how much taller is the left square than the right?
Solve It! The diagram shows two adjacent squares and their areas. In terms of x, how much taller is the left square than the right?
8 points
8
Question 2
2.
Take Note: Factoring Perfect-Square Trinomials
x^{2}+8x+16=(x+4)(x+4)=(__________)^{2}
4n^{2}-12n+9=(__________)(__________)=(2n-3)^2
x^{2}+10x+25=(__________)^2
10 points
10
Question 3
3.
Problem 1 Got It?
Problem 1 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 4
4.
Problem 1 Got It?
Problem 1 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 5
5.
Problem 2 Got It?
Problem 2 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 6
6.
Take Note: Vocabulary: Which of the following binomials are differences of squares? Select all that apply.
Take Note: Vocabulary: Which of the following binomials are differences of squares? Select all that apply.
10 points
10
Question 7
7.
Take Note: Vocabulary: Write a simplified binomial that is a difference of squares.
Take Note: Vocabulary: Write a simplified binomial that is a difference of squares.
8 points
8
Question 8
8.
Take Note: Factoring a Difference of Two Squares
x^{2}-25=(x__________5)(x__________5)
4x^{2}-100=(__________)(__________)
10 points
10
Question 9
9.
Problem 3 Got It?
Problem 3 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 10
10.
Problem 3 Got It?
Problem 3 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 11
11.
Problem 4 Got It? What is the factored form of the binomial?
Problem 4 Got It? What is the factored form of the binomial?
Enter only a simplified expression with two binomials.
A.SSE.1.a
A.SSE.1.b
A.SSE.2
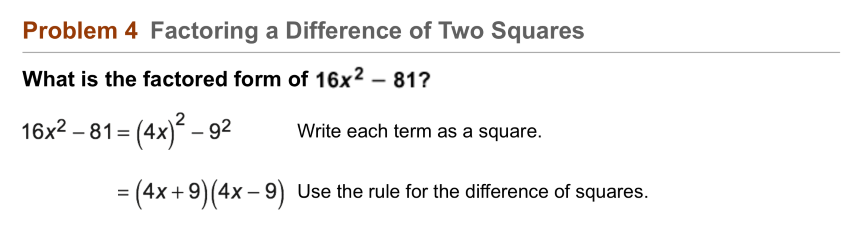
10 points
10
Question 12
12.
Problem 4 Got It? Reasoning: The expression below contains two perfect squares.
Problem 4 Got It? Reasoning: The expression below contains two perfect squares.
Can you use the method in Problem 4 to factor it? Explain your reasoning.
6 points
6
Question 13
13.
Match each expression with its greatest common factor (GCF).
Take Note: GCF Review
Match each expression with its greatest common factor (GCF).
| arrow_right_alt | 6 | |
| arrow_right_alt | 3x | |
| arrow_right_alt | 2 |
10 points
10
Question 14
14.
Problem 5 Got It?
Problem 5 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 15
15.
Problem 5 Got It?
Problem 5 Got It?
A.SSE.1.a
A.SSE.1.b
A.SSE.2
10 points
10
Question 16
16.
Take Note: Summarize the mathematical content of this lesson. What topics, ideas, and vocabulary were introduced?
Take Note: Summarize the mathematical content of this lesson. What topics, ideas, and vocabulary were introduced?