Algebra 2 7-3 Guided Practice: Logarithmic Functions as Inverses
star
star
star
star
star
Last updated about 3 years ago
31 questions
3
12
3
3
3
3
10
10
…
3
9
18
…







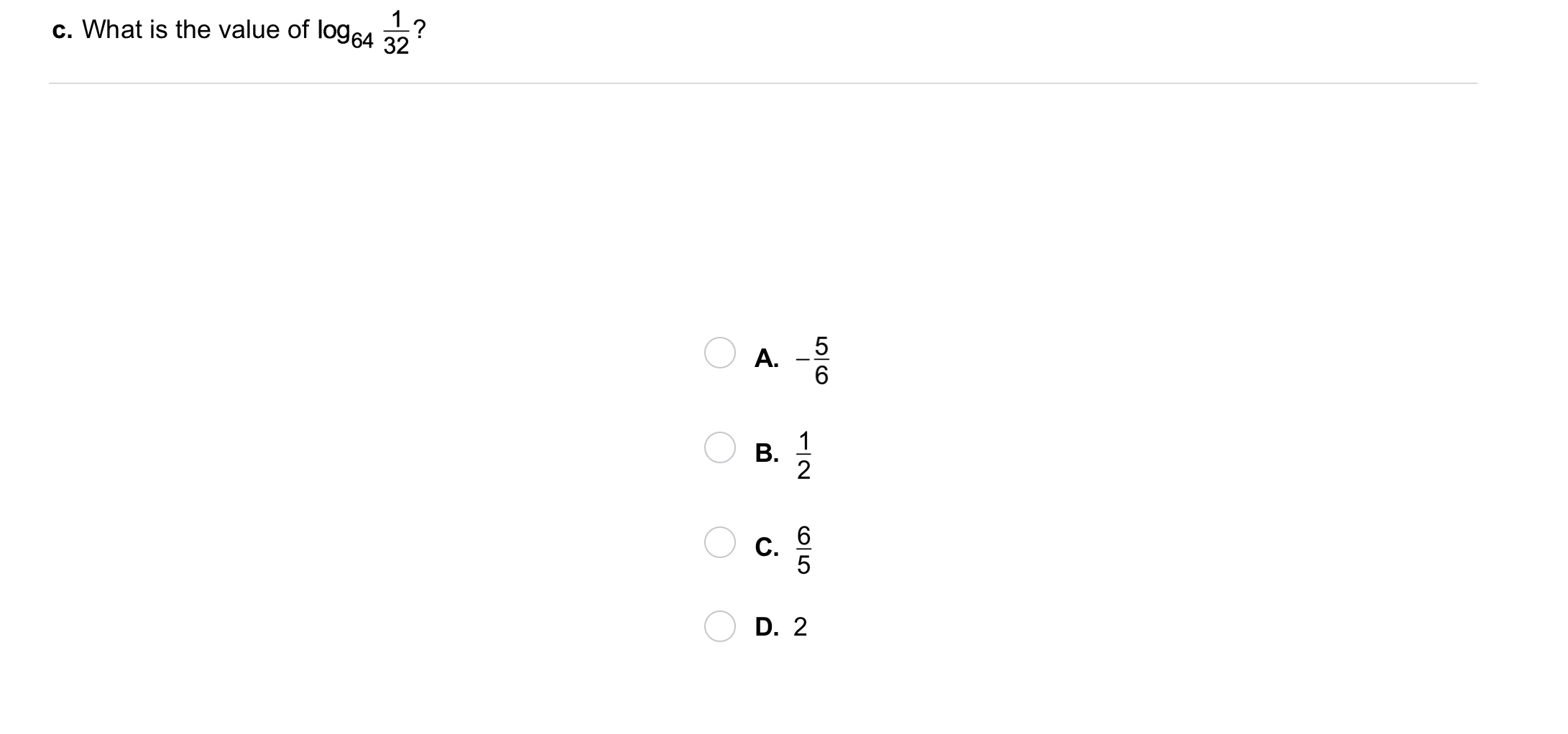


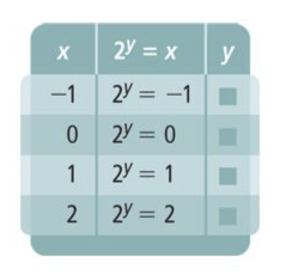
| Draggable item | arrow_right_alt | Corresponding Item |
|---|---|---|
horizontal translation (shift) | arrow_right_alt | a |
vertical translation (shift) | arrow_right_alt | h |
vertical scaling (stretch/compression) & reflection (flip) | arrow_right_alt | k |
