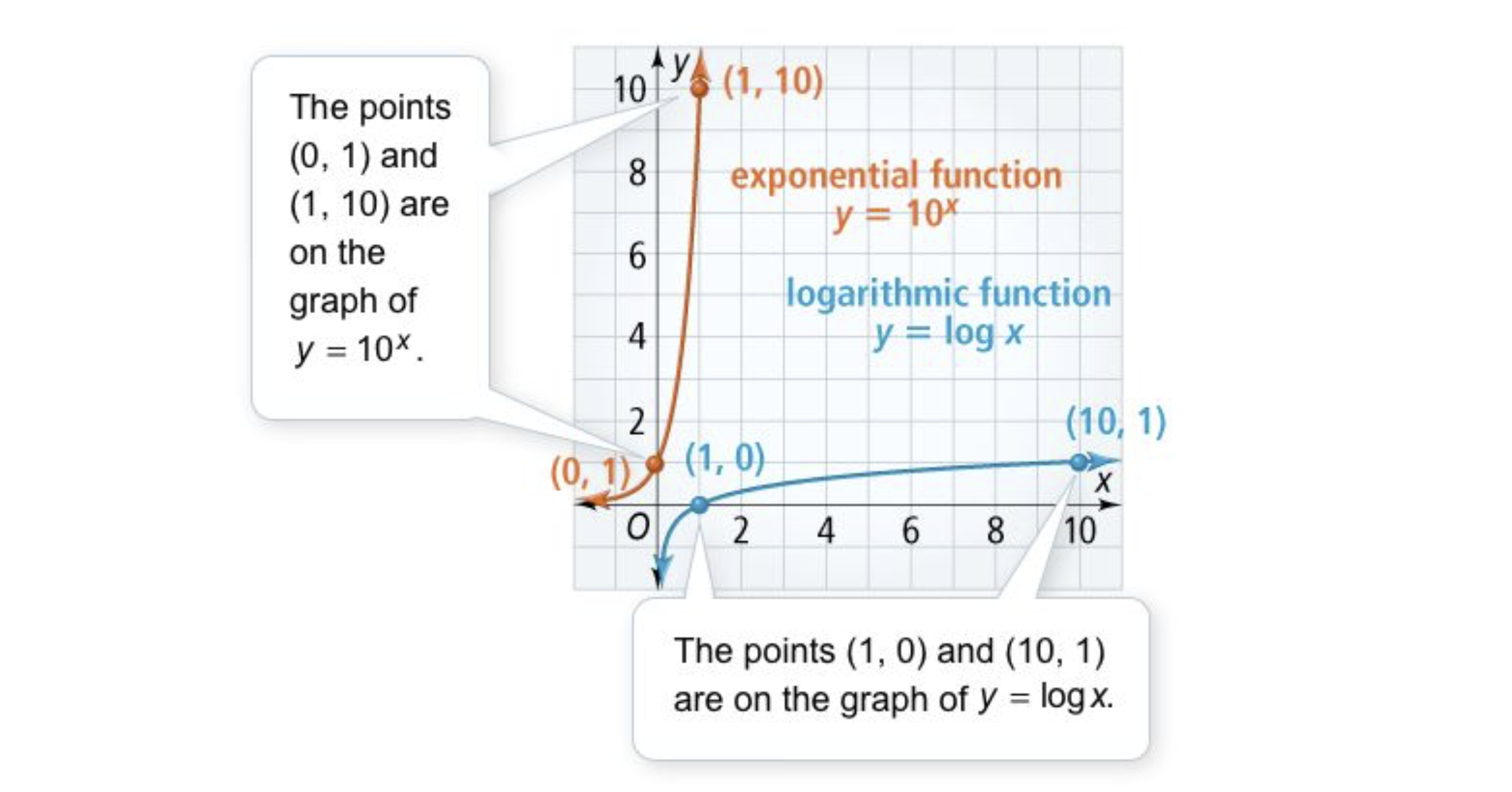
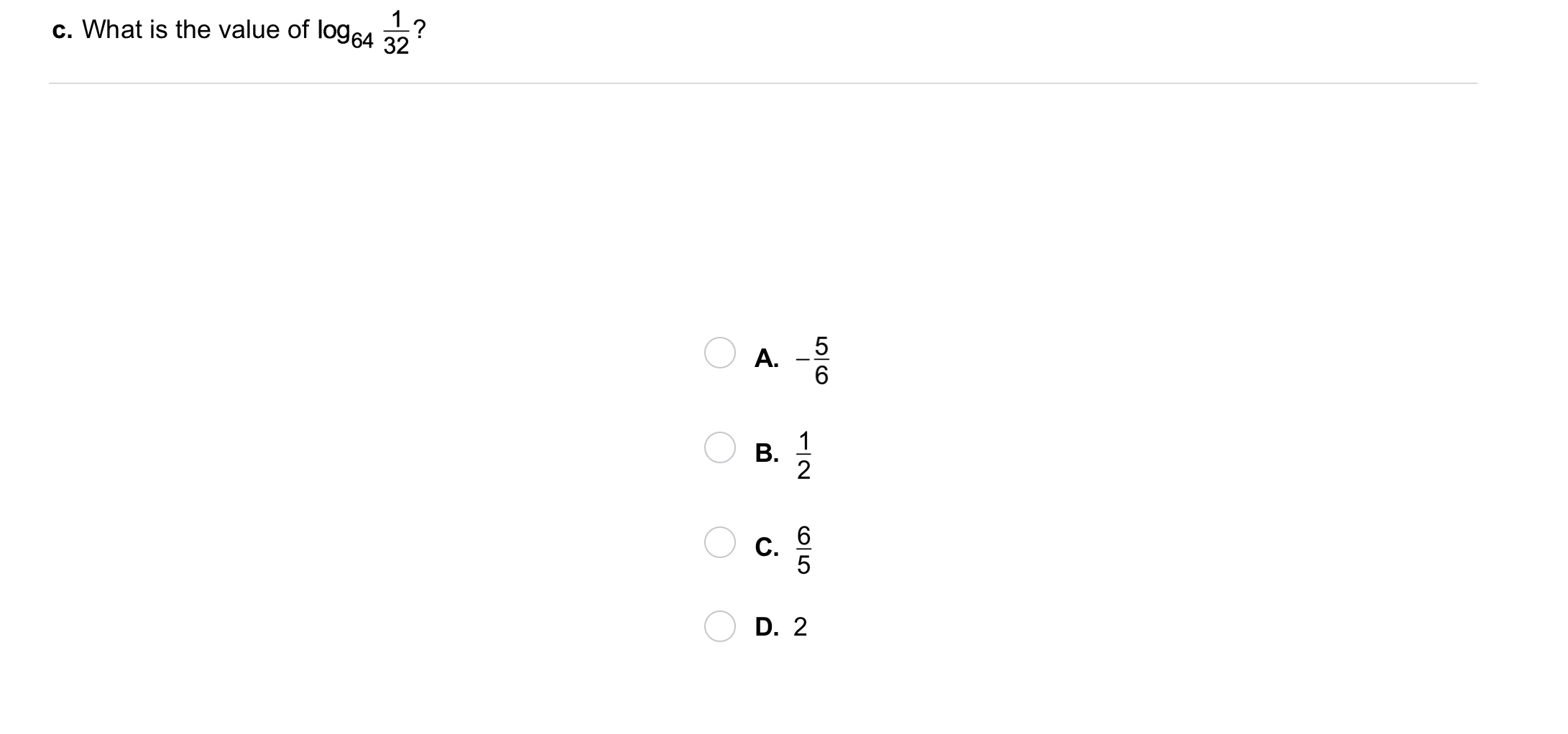
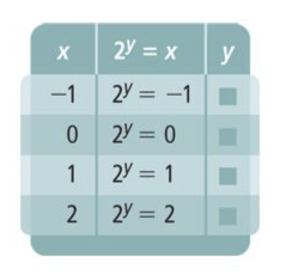
Algebra 2 7-3 Complete Lesson: Logarithmic Functions as Inverses
star
star
star
star
star
Last updated about 4 years ago
38 questions
Note from the author:
A complete formative lesson with embedded slideshow, mini lecture screencasts, checks for understanding, practice items, mixed review, and reflection. I create these assignments to supplement each lesson of Pearson's Common Core Edition Algebra 1, Algebra 2, and Geometry courses. See also mathquest.net and twitter.com/mathquestEDU.
10
10
…
21
…
5
5
5
5
10
…
20
5
5
5
10
10
10
10
10
100
10
…