Geometry 3-5 Complete Lesson: Parallel Lines and Triangles
By Matt Richardson
starstarstarstarstarstarstarstarstarstar
Last updated about 3 years ago
27 Questions
Note from the author:
A complete formative lesson with embedded slideshow, mini lecture screencasts, checks for understanding, practice items, mixed review, and reflection. I create these assignments to supplement each lesson of Pearson's Common Core Edition Algebra 1, Algebra 2, and Geometry courses. See also mathquest.net and twitter.com/mathquestEDU.
30 points
30
Question 1
1.
Solve It! Complete the following steps. Take and upload pictures to the canvas to document your progress after each step.
1. Draw and cut out a large triangle.2. Tear off all three corners of the triangle.3. Place the three corner pieces (that you tore off) so that they form adjacent angles.
Solve It! Complete the following steps. Take and upload pictures to the canvas to document your progress after each step.
1. Draw and cut out a large triangle.
2. Tear off all three corners of the triangle.
3. Place the three corner pieces (that you tore off) so that they form adjacent angles.
10 points
10
Question 2
2.
Solve It! What is the sum of the meaures of the three angles of your triangle?Enter only a number.
Solve It! What is the sum of the meaures of the three angles of your triangle?
Enter only a number.
10 points
10
Question 3
3.
Solve It! Do all triangles have the same interior angle sum? How does the Solve It! activity support your answer?
Solve It! Do all triangles have the same interior angle sum? How does the Solve It! activity support your answer?
10 points
10
Question 4
4.
Take Note: Summarize The Parallel Postulate. You may use the canvas to help illustrate your explanation.
Take Note: Summarize The Parallel Postulate. You may use the canvas to help illustrate your explanation.
10 points
10
Question 5
5.
Take Note: Summarize Theorem 3-11. You may use the canvas to help illustrate your explanation.
Take Note: Summarize Theorem 3-11. You may use the canvas to help illustrate your explanation.
10 points
10
Question 6
6.
Take Note: Define auxiliary line. You may use the canvas to help illustrate your explanation.
Take Note: Define auxiliary line. You may use the canvas to help illustrate your explanation.
10 points
10
Question 7
7.
Problem 1 Got It?
Problem 1 Got It?
10 points
10
Question 8
8.
Take Note: Define remote interior angles. You may use the canvas to help illustrate your description.
Take Note: Define remote interior angles. You may use the canvas to help illustrate your description.
10 points
10
Question 9
9.
Take Note: Summarize The Triangle Exterior Angle Theorem. You may use the canvas to help illustrate your description.
Take Note: Summarize The Triangle Exterior Angle Theorem. You may use the canvas to help illustrate your description.
10 points
10
Question 10
10.
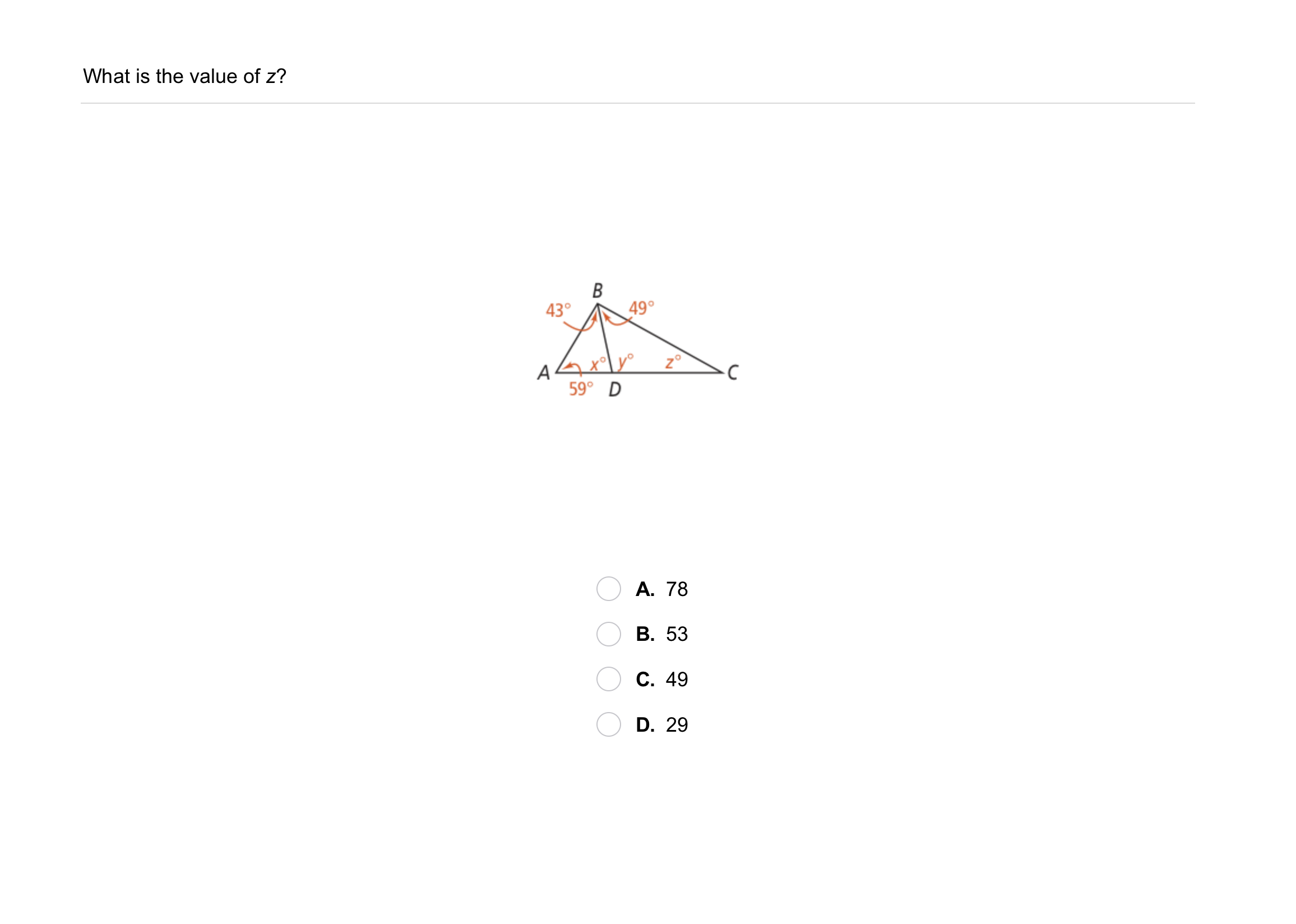
Problem 2 Got It? Two angles of a triangle measure 53. What is the measure of an exterior angle at each vertex of the triangle?
Problem 2 Got It? Two angles of a triangle measure 53. What is the measure of an exterior angle at each vertex of the triangle?
10 points
10
Question 11
11.
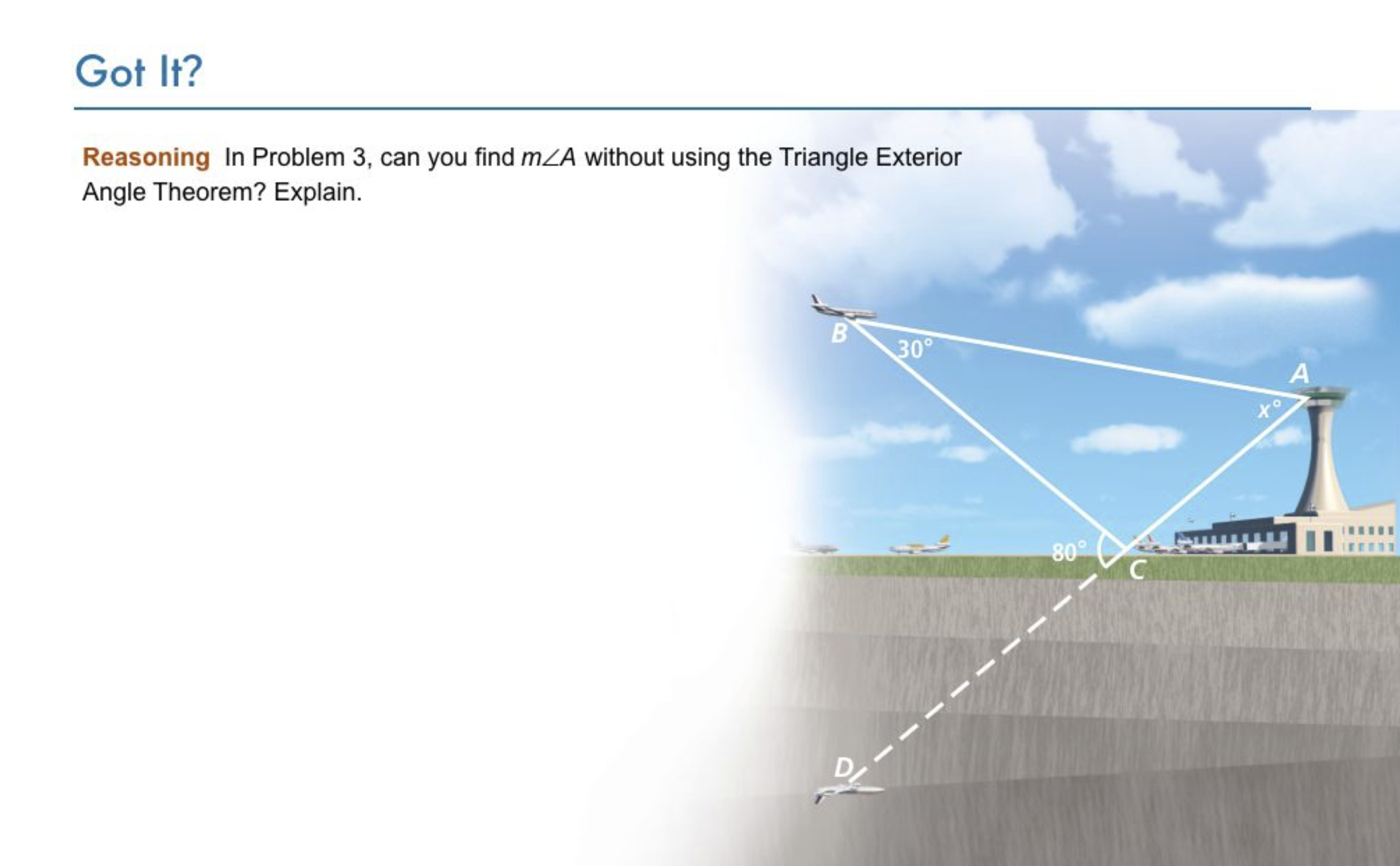
Problem 3 Got It? In Problem 3, can you find m∠A without using the Triangle Exterior Angle Theorem?
Problem 3 Got It? In Problem 3, can you find m∠A without using the Triangle Exterior Angle Theorem?
10 points
10
10 points
10
Question 13
13.
10 points
10
Question 14
14.
10 points
10
Question 15
15.
10 points
10
Question 16
16.
10 points
10
Question 17
17.
10 points
10
Question 18
18.
10 points
10
Question 19
19.
Reasoning: Explain how the Triangle Exterior Angle Theorem makes sense based on the Triangle Angle-Sum Theorem.
Reasoning: Explain how the Triangle Exterior Angle Theorem makes sense based on the Triangle Angle-Sum Theorem.
10 points
10
Question 20
20.
Error Analysis: The measures of the interior angles of a triangle are 30, x, and 3x. Which of these methods for solving for x is incorrect?
Error Analysis: The measures of the interior angles of a triangle are 30, x, and 3x. Which of these methods for solving for x is incorrect?
10 points
10
Question 21
21.
Explain.
Explain.
5 points
5
Question 22
22.
Review Lesson 3-4: If ∠1 and ∠2 are supplementary, what can you conclude about lines a and c?
Review Lesson 3-4: If ∠1 and ∠2 are supplementary, what can you conclude about lines a and c?
10 points
10
Question 23
23.
Review Lesson 3-4: ∠ABC and ∠CBD form a linear pair. If m∠ABC = 3x + 20 and m∠CBD = x + 32, find the value of x. Enter only a number.
Review Lesson 3-4: ∠ABC and ∠CBD form a linear pair. If m∠ABC = 3x + 20 and m∠CBD = x + 32, find the value of x. Enter only a number.
10 points
10
Question 24
24.
Review Lesson 3-4: ∠1 and ∠2 are supplementary. If ∠1 ≅ ∠2, find m∠1 and m∠2. Enter only a number.
Review Lesson 3-4: ∠1 and ∠2 are supplementary. If ∠1 ≅ ∠2, find m∠1 and m∠2. Enter only a number.
10 points
10
Question 25
25.
Vocabulary Review: Identify the part of speech for the word alternate in each sentence on the right.
Vocabulary Review: Identify the part of speech for the word alternate in each sentence on the right.
- NOUN
- ADJECTIVE
- VERB
- You vote for one winner an one alternate.
- Your two friends alternate serves during tennis.
- You and your sister babysit on alternate nights.
10 points
10
Question 26
26.
Use Your Vocabulary: Classify each statement as true or false.
Use Your Vocabulary: Classify each statement as true or false.
- A triangle is a polygon with three or more sides.
- A tripod is a stand that has three legs.
- In order to triple an amount, multiply it by three.
- A triathlon is a race with two events - swimming & bicycling.
- True
- False
10 points
10
Question 27
27.
Reflection: Math Success
Reflection: Math Success