Illustrative Math - Algebra 2 - Unit 2 - Lesson 2
star
star
star
star
star
Last updated 9 months ago
10 questions
1
Select all polynomial expressions that are equivalent to 6x^{4}+4x^{3}-7x^{2}+5x+8.
Select all polynomial expressions that are equivalent to 6x^{4}+4x^{3}-7x^{2}+5x+8.
…

1
1
1
Consider the polynomial function p given by p(x)=5x^{3}+8x^{2}-3x+1. Evaluate the function at x=-2.
Consider the polynomial function p given by p(x)=5x^{3}+8x^{2}-3x+1. Evaluate the function at x=-2.
…
1
An open-top box is formed by cutting squares out of a 5 inch by 7 inch piece of paper and then folding up the sides. The volume V(x) in cubic inches of this type of open-top box is a function of the side length x in inches of the square cutouts and can be given by V(x)=(7-2x)(5-2x)(x). Rewrite this equation by expanding the polynomial.
An open-top box is formed by cutting squares out of a 5 inch by 7 inch piece of paper and then folding up the sides. The volume V(x) in cubic inches of this type of open-top box is a function of the side length x in inches of the square cutouts and can be given by V(x)=(7-2x)(5-2x)(x). Rewrite this equation by expanding the polynomial.
…

1
1
1
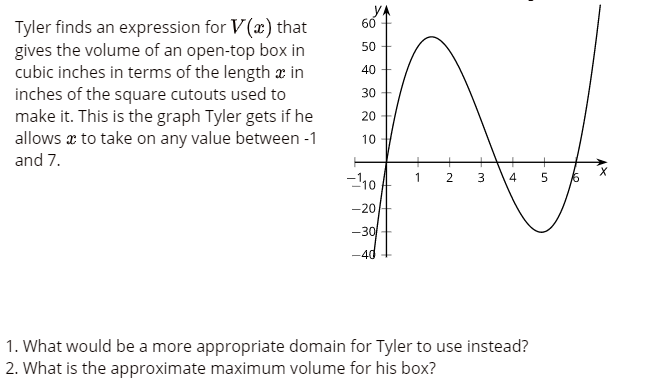
1
1