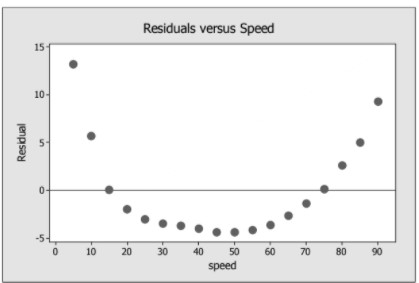
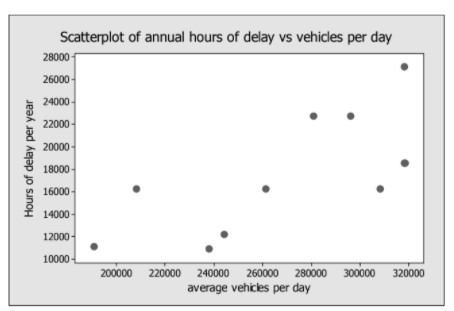
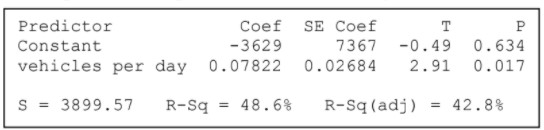
AP Statistics Chapter 3 TEST
star
star
star
star
star
Last updated about 5 years ago
14 questions
Note from the author:
Based on The Practice of Statistics, 4th edition teacher resources. Some questions were adjusted/modified.
1
1
1
1
1
1
1
1
1
1
4
2
2
2