Log inSign up for FREE
Library

Unit 4 Practice Test

Last updated over 1 year ago
21 questions
1

Classify the triangle by its sides and angles.

1

Given 2 triangles with 3-pairs of corresponding, congruent sides, what theorem would you use to prove the triangles congruent

1

If triangle ABC is congruent to triangle RPQ, then what is the measure of angle P?

1

If triangle ABC is congruent to trianlge RPQ, then segment AB is congruent to...?

1

If triangle ABC is congruent to trianlge RPQ, then triangle CBA is congruent to...?
Note: Your answer must be in the correct order.

1

Can you prove triangle ABC is congruent to triangle EDC by one of the following theorems?

1

Can you prove triangle KJL is congruent to triangle MLJ by one of the following theorems?

1

How would you conclude that triangle JKM is congruent to triangle LKM?

1

If segment HD is parallel to segment FG, then which of the following statements would be true?

1

Classify the triangle by its sides and angles.
Hint: Perpendiular lines have slopes with a product of -1.

2

What is the value of the exterior angle?
Hint: exterior angle = sum of interior angles.

1

Determine the value of x.

1

Determine the value of x.

1

Determine the value of x.

3

Prove that triangle ABC is congruent to triangle DEC by matching the statements to the correct reasons.

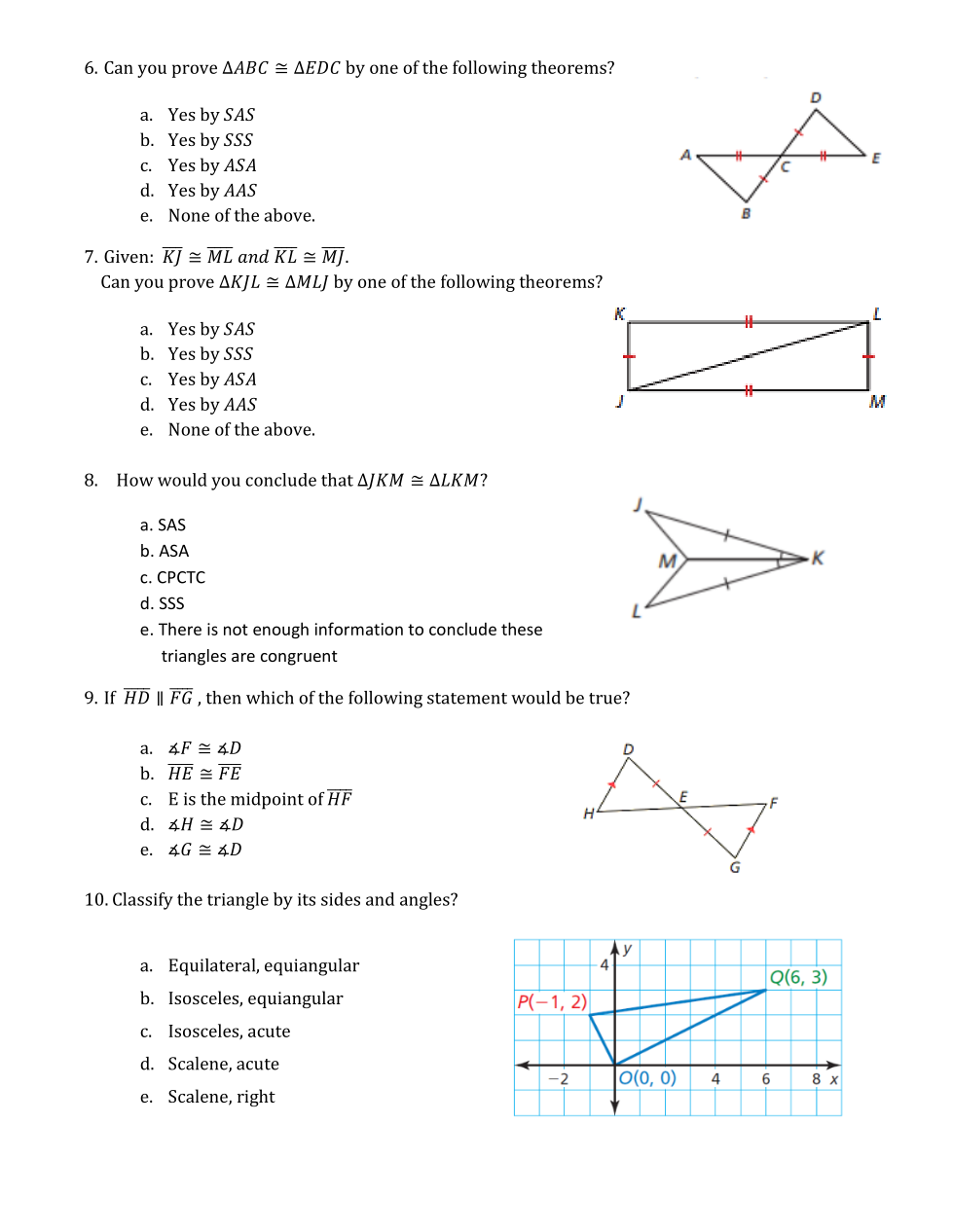
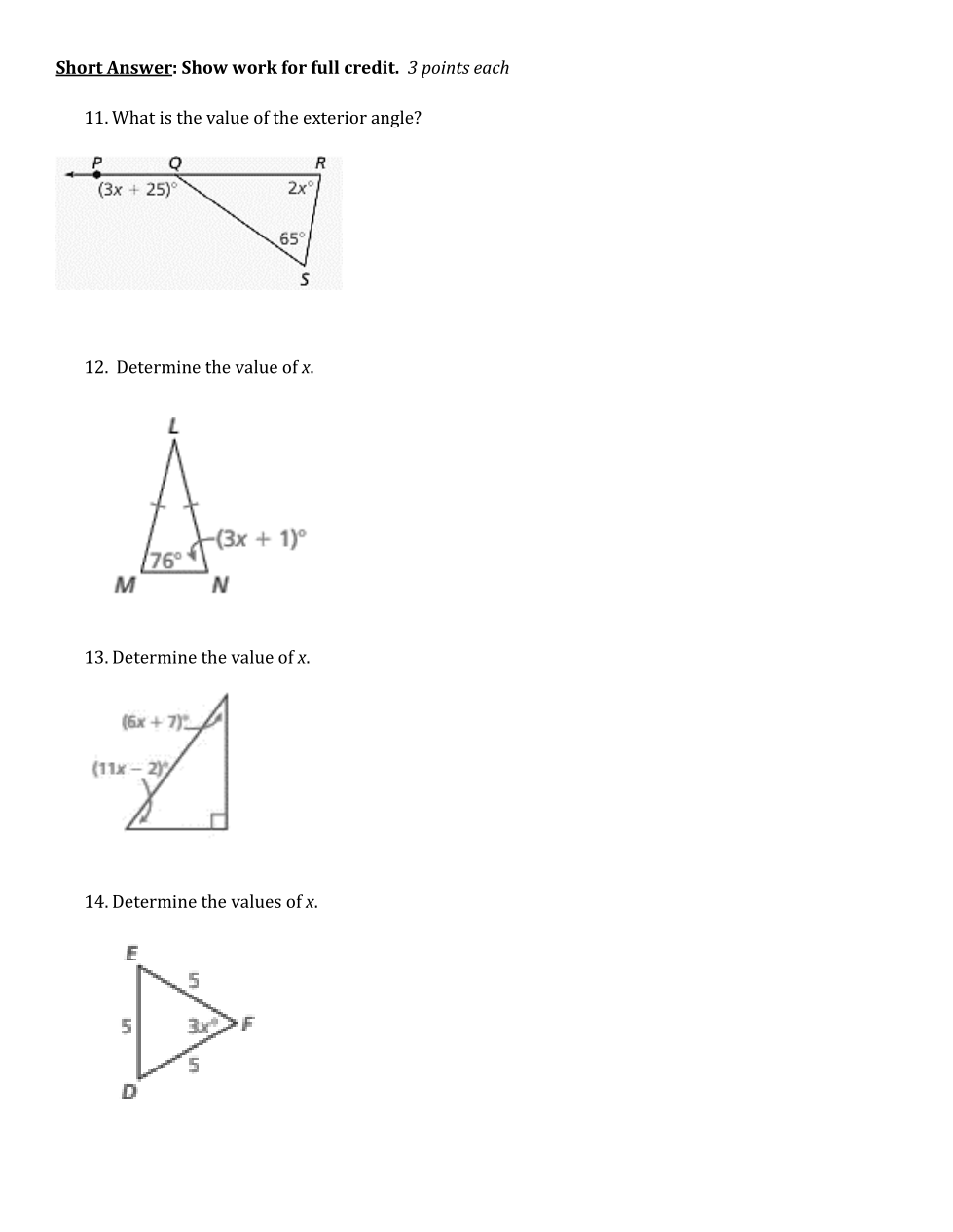
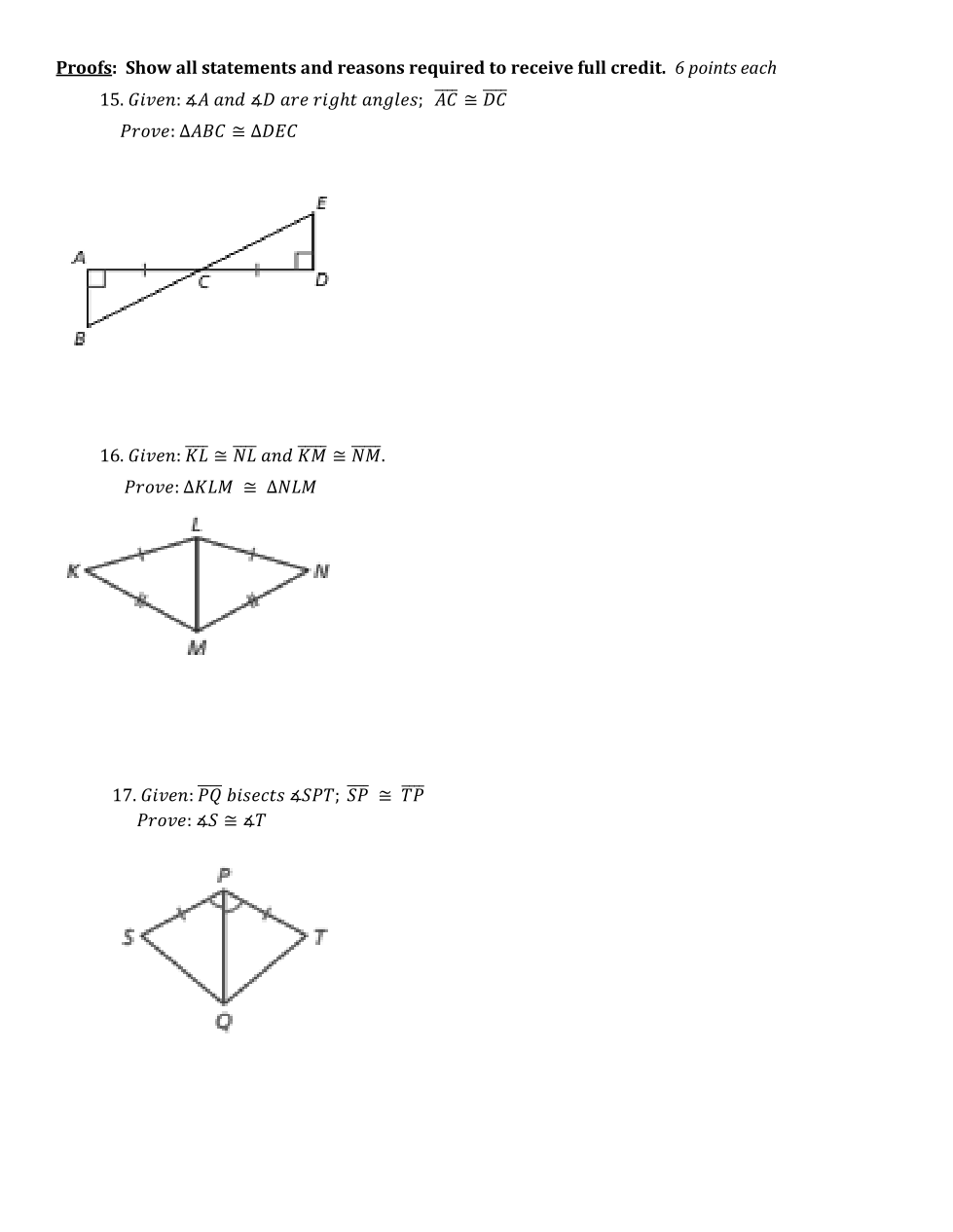
Draggable itemCorresponding Item
are right angles.
Given Fact
All right angles are congruent.


Given Fact
Vertical angles are congruent.
ASA Theorem
2

Prove that triangle KLM is congruent to triangle NLM by putting the steps of the following proof in logical order.

  1. (Reflexive Property)
  2. (Given Fact)
  4. (Given Fact)
For problems 17 - 21, justify each step of the following proof.

Given:
Prove:

1

Justify the statements:
and

1

Justify the statement:

1

Justify the statement:

1

Justify the statement:

1

Justify the statement: