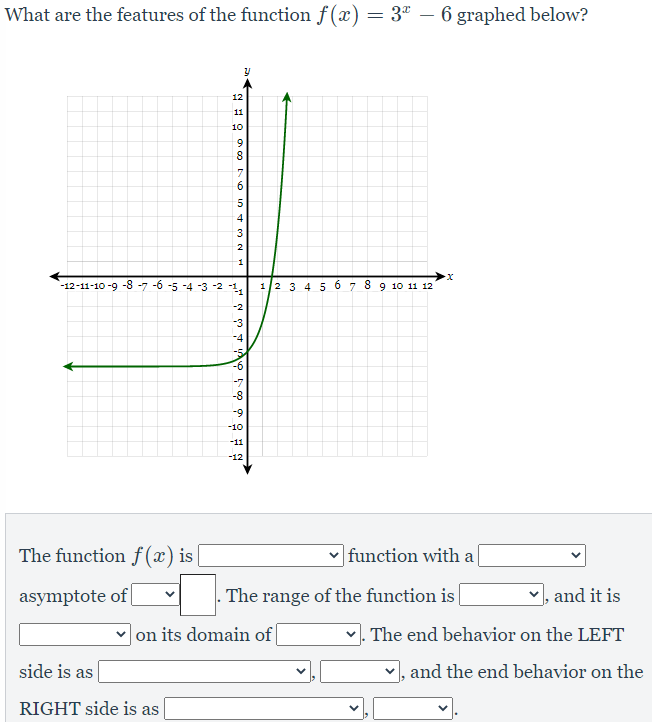
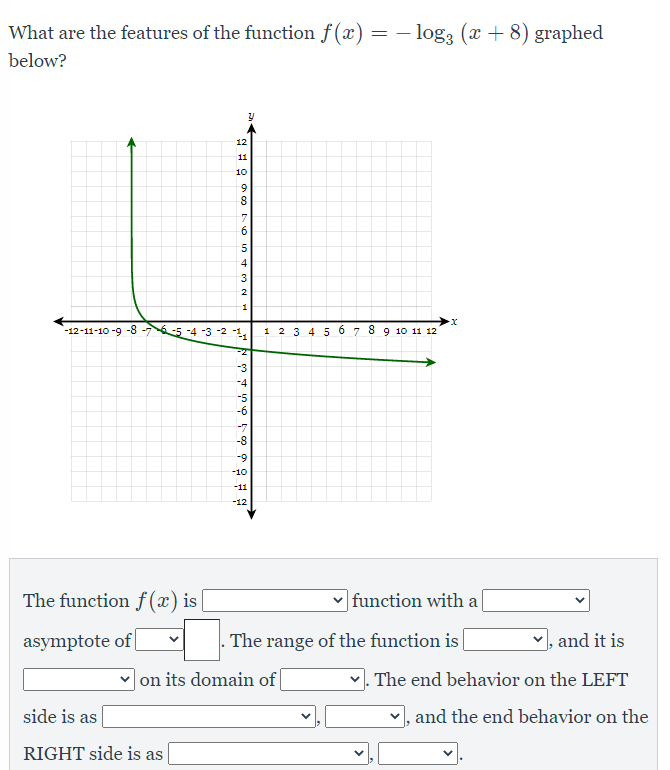
The accompanying table shows the value of a car over time that was purchased for 18500 dollars, where x is years and y is the value of the car in dollars. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest ten-thousandth.