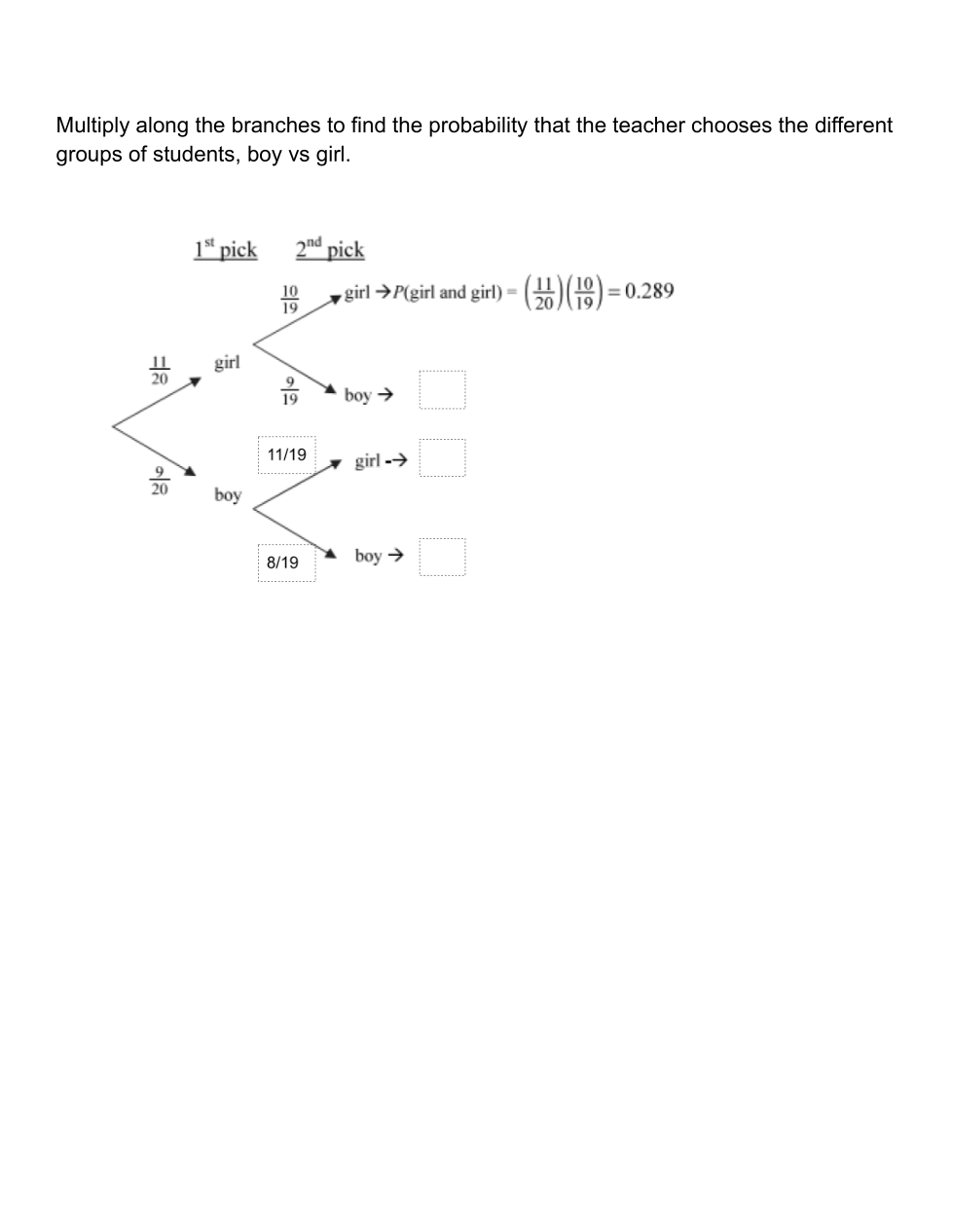
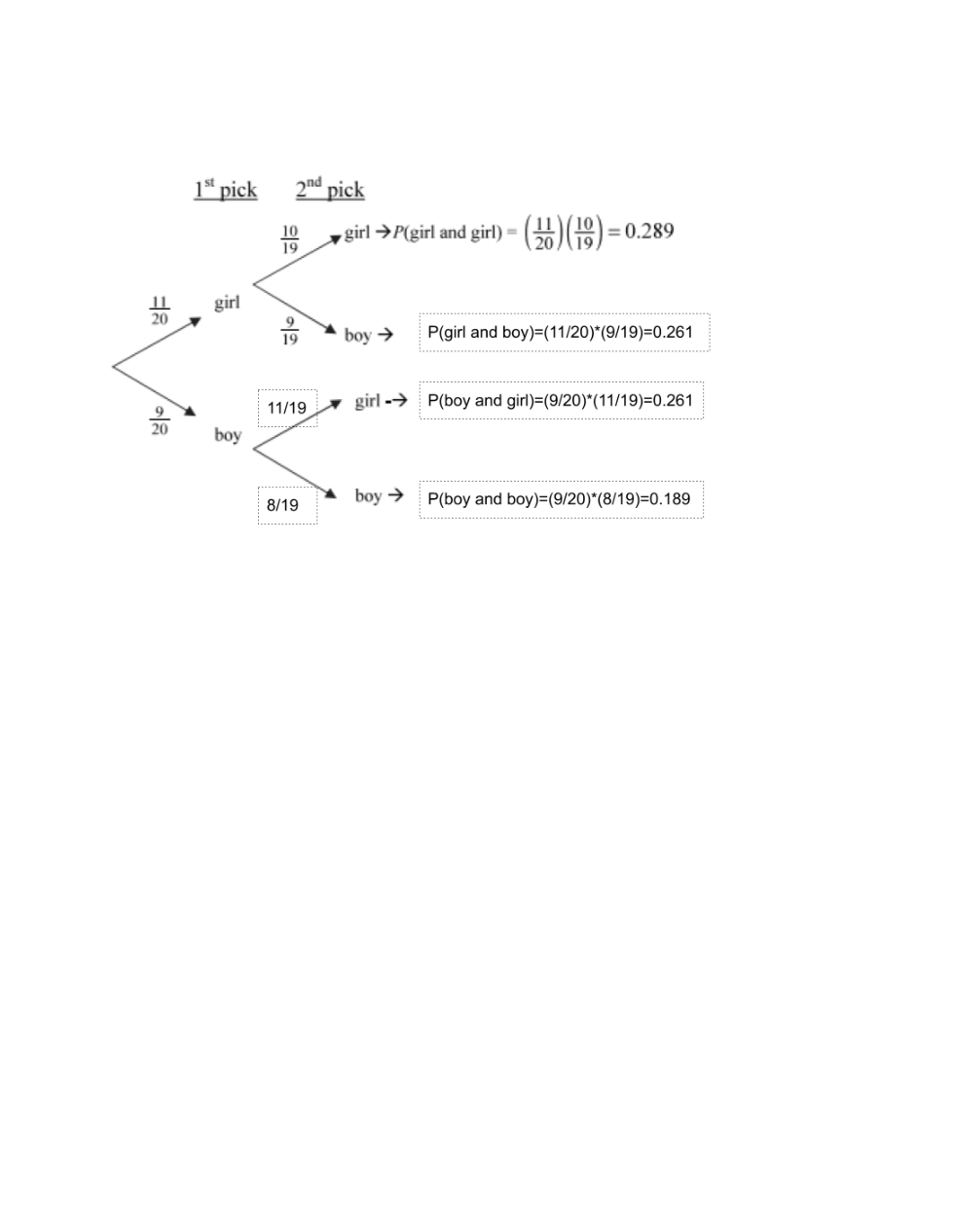
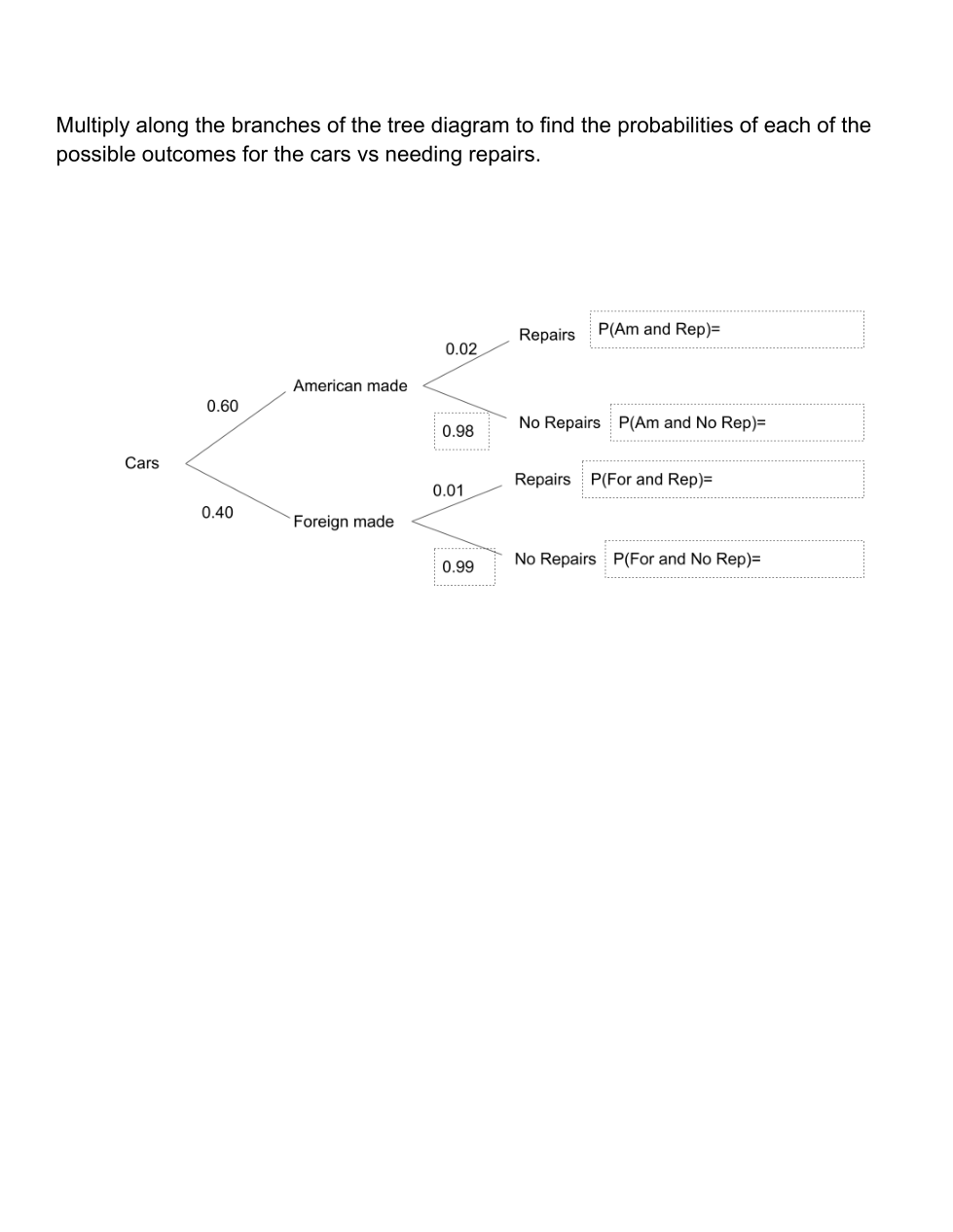
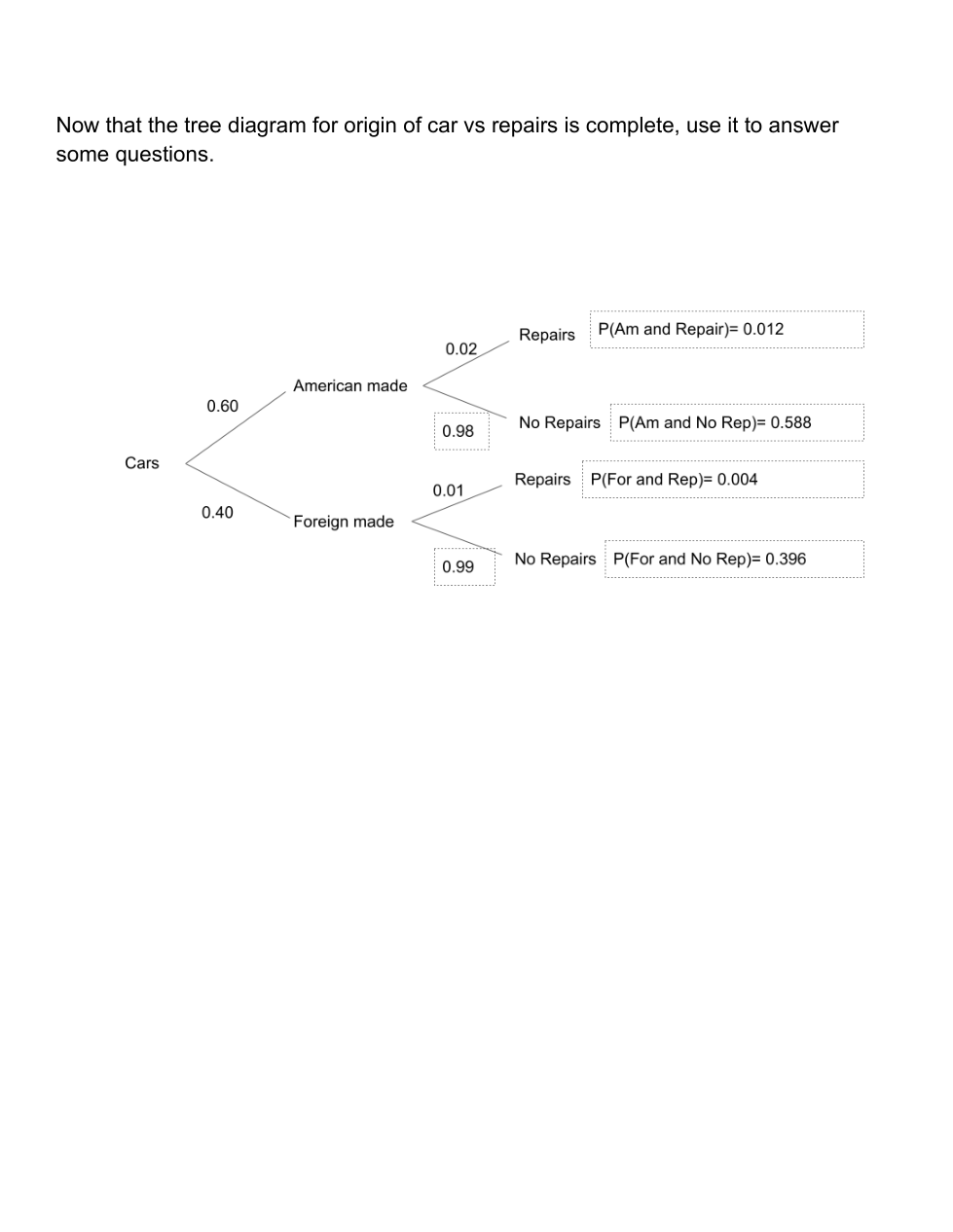
Unit 9 Day 3 Tree Diagram Practice
star
star
star
star
star
Last updated over 4 years ago
25 questions
4
4
4
4
4
"Suppose that 5 percent of bags contain forbidden items."
"If a bag contains a forbidden item, there is a 98 percent chance that it triggers the alarm."
"If a bag doesn't contain a forbidden item, there is an 8 percent chance that it triggers the alarm."