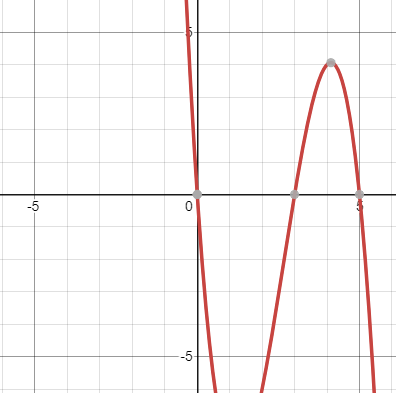
Quiz 5.1 - Ops, Features, and Roots
star
star
star
star
star
Last updated almost 4 years ago
16 questions
Note from the author:
For the ones that don't give you a specific polynomial, it may be helpful to make up your own that fits the description.
For the ones that don't give you a specific polynomial, it may be helpful to make up your own that fits the description.
1
1
1
1
1
1
1
1
1
1
1
1
1
1