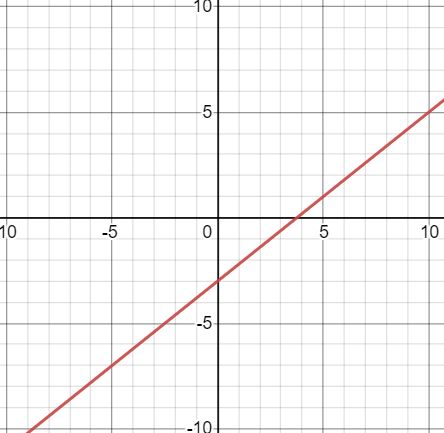
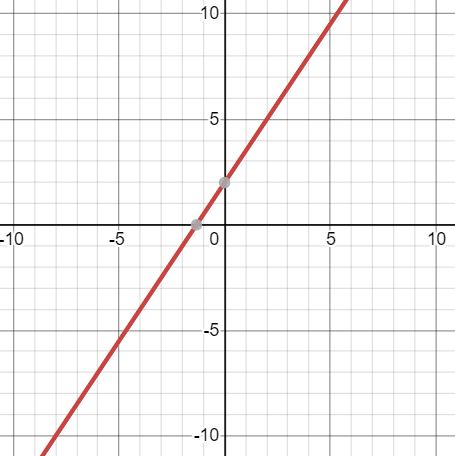
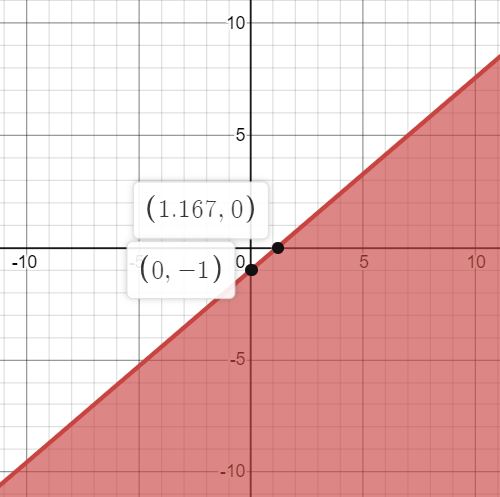
A triathlon consists of swimming, biking, and running. There are different sizes for the event, but usually contestants run about 7 times the distance that they swim. An Olympic triathlon is 51.5 km long. Write an equation, with x as the swimming distance, and y as the biking distance, to represent the situation.