Eureka Grade 6 Module 3 End-Module Test

Last updated almost 4 years ago

20 questions

Required

6.NS.6.c

Required

6.NS.6.b

Required

6.NS.6.b

6.NS.8

Required

6.NS.6.c

Required

6.NS.6.a

6.NS.7.c

Required

6.NS.8

6.NS.6.b

6.NS.8

MP.1

6.NS.8

6.NS.6.b

	Quadrant I	Quadrant II	Quadrant III	Quadrant IV
The green circle is in
The blue pentagon is in
The yellow square is in
The red triangle is in
The point (4, --2) is in
The reflection over the y-axis of point (--3, 5) is in
If both numbers in an ordered pair are negative, the point is in

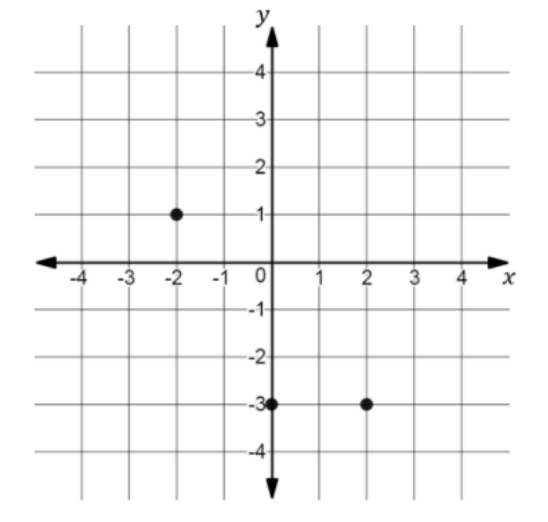
	TRUE	FALSE
The x-coordinates have the same absolute value
The x-coordinates are opposite numbers
Both points are 5 units away from the y-axis
The points lie on opposite sides of each axis
One point is 2 units right of the y-axis

Eureka Grade 6 Module 3 End-Module Test

Eureka Grade 6 Module 3 End-Module Test

Graph and label each point on the coordinate plane.
A) (7, --5)
B) (4, 5)
C) (--3, --4)
D) (2, 0)
E) (--6, 7)

The coordinates of point A are

Write the coordinates for Point A [use format (x,y)]

Write the coordinates for Point B [use format (x,y)]

Point A is located at (-4, 9) on the coordinate plane. Point B is located at (--4, --7).
What is the distance between Point A and Point B? Your answer should be in units.

Use the information below to plot and label John’s fourth point.
Neither coordinate of John’s fourth point is negative.
The horizontal distance between John’s fourth point and one of his other points is 2.

Plot the points (-2, -5) and (2, 5) in the coordinate plane.

Use your work in Question 14 to say whether each statement is TRUE or FALSE

The coordinates of two vertices (corners) of a rectangle are (3, 3) and (--5, 3). If the rectangle has a
perimeter (distance around the outside) of 30 units, what are the possible coordinates of its other two vertices?

CHALLENGE QUESTION I
On a coordinate plane Mitchell’s house is located at (--5,2). Liam’s house is located at a point that is a reflection of Mitchell’s house over the y-axis. What are the coordinates of Liam’s house? Use the coordinate plane to help you think about the problem.

CHALLENGE QUESTION II
What is the distance between Mitchell and Liam’s house? (Answer in units: for example "2 units")

CHALLENGE QUESTION III
What would the coordinates of Mitchell’s house be if it was reflected over the x-axis?

CHALLENGE QUESTION IV
What would the coordinates be if Mitchell's house was reflected over the origin? Note: this is what Mr. Randolph calls a "double reflection," where the point is reflected over the x-axis AND over the y-axis.

Graph and label each point on the coordinate plane.
A) (7, --5)
B) (4, 5)
C) (--3, --4)
D) (2, 0)
E) (--6, 7)

Drag a point on the LEFT to the matching reflection definition (there will be only one per definition). Drag all the others to the "no match" group.

The coordinates of point A are

The coordinates of point B are

Point C has the same first coordinate as Point A
The second coordinate of Point C is 1/2 the second coordinate of Point B
What are the coordinates of Point C?

Locate and label point C on the coordinate plane.

Write the coordinates for Point A [use format (x,y)]

Write the coordinates for Point B [use format (x,y)]

Write the coordinates for Point C [use format (x,y)]

Use the image to

Point A is located at (-4, 9) on the coordinate plane. Point B is located at (--4, --7).
What is the distance between Point A and Point B? Your answer should be in units.

Use the information below to plot and label John’s fourth point.
Neither coordinate of John’s fourth point is negative.
The horizontal distance between John’s fourth point and one of his other points is 2.

Which statement(s) about John’s points are true?
Select all that apply.

Plot the points (-2, -5) and (2, 5) in the coordinate plane.

Use your work in Question 14 to say whether each statement is TRUE or FALSE

The coordinates of two vertices (corners) of a rectangle are (3, 3) and (--5, 3). If the rectangle has a
perimeter (distance around the outside) of 30 units, what are the possible coordinates of its other two vertices?

CHALLENGE QUESTION I
On a coordinate plane Mitchell’s house is located at (--5,2). Liam’s house is located at a point that is a reflection of Mitchell’s house over the y-axis. What are the coordinates of Liam’s house? Use the coordinate plane to help you think about the problem.

CHALLENGE QUESTION II
What is the distance between Mitchell and Liam’s house? (Answer in units: for example "2 units")

CHALLENGE QUESTION III
What would the coordinates of Mitchell’s house be if it was reflected over the x-axis?

CHALLENGE QUESTION IV
What would the coordinates be if Mitchell's house was reflected over the origin? Note: this is what Mr. Randolph calls a "double reflection," where the point is reflected over the x-axis AND over the y-axis.

The coordinates of point B are

Point C has the same first coordinate as Point A
The second coordinate of Point C is 1/2 the second coordinate of Point B
What are the coordinates of Point C?

Locate and label point C on the coordinate plane.

Write the coordinates for Point C [use format (x,y)]

Which statement(s) about John’s points are true?
Select all that apply.

Eureka Grade 6 Module 3 End-Module Test

Eureka Grade 6 Module 3 End-Module Test

Graph and label each point on the coordinate plane. A) (7, --5)B) (4, 5)C) (--3, --4)D) (2, 0)E) (--6, 7)

The coordinates of point A are

Write the coordinates for Point A [use format (x,y)]

Write the coordinates for Point B [use format (x,y)]

Point A is located at (-4, 9) on the coordinate plane. Point B is located at (--4, --7).What is the distance between Point A and Point B? Your answer should be in units.

Use the information below to plot and label John’s fourth point.Neither coordinate of John’s fourth point is negative.The horizontal distance between John’s fourth point and one of his other points is 2.

Plot the points (-2, -5) and (2, 5) in the coordinate plane.

Use your work in Question 14 to say whether each statement is TRUE or FALSE

The coordinates of two vertices (corners) of a rectangle are (3, 3) and (--5, 3). If the rectangle has aperimeter (distance around the outside) of 30 units, what are the possible coordinates of its other two vertices?

CHALLENGE QUESTION IOn a coordinate plane Mitchell’s house is located at (--5,2). Liam’s house is located at a point that is a reflection of Mitchell’s house over the y-axis. What are the coordinates of Liam’s house? Use the coordinate plane to help you think about the problem.

CHALLENGE QUESTION IIWhat is the distance between Mitchell and Liam’s house? (Answer in units: for example "2 units")

CHALLENGE QUESTION IIIWhat would the coordinates of Mitchell’s house be if it was reflected over the x-axis?

CHALLENGE QUESTION IVWhat would the coordinates be if Mitchell's house was reflected over the origin? Note: this is what Mr. Randolph calls a "double reflection," where the point is reflected over the x-axis AND over the y-axis.

Graph and label each point on the coordinate plane. A) (7, --5)B) (4, 5)C) (--3, --4)D) (2, 0)E) (--6, 7)

Drag a point on the LEFT to the matching reflection definition (there will be only one per definition). Drag all the others to the "no match" group.

The coordinates of point A are

The coordinates of point B are

Point C has the same first coordinate as Point AThe second coordinate of Point C is 1/2 the second coordinate of Point BWhat are the coordinates of Point C?

Locate and label point C on the coordinate plane.

Write the coordinates for Point A [use format (x,y)]

Write the coordinates for Point B [use format (x,y)]

Write the coordinates for Point C [use format (x,y)]

Use the image to

Point A is located at (-4, 9) on the coordinate plane. Point B is located at (--4, --7).What is the distance between Point A and Point B? Your answer should be in units.

Use the information below to plot and label John’s fourth point.Neither coordinate of John’s fourth point is negative.The horizontal distance between John’s fourth point and one of his other points is 2.

Which statement(s) about John’s points are true?Select all that apply.

Plot the points (-2, -5) and (2, 5) in the coordinate plane.

Use your work in Question 14 to say whether each statement is TRUE or FALSE

The coordinates of two vertices (corners) of a rectangle are (3, 3) and (--5, 3). If the rectangle has aperimeter (distance around the outside) of 30 units, what are the possible coordinates of its other two vertices?

CHALLENGE QUESTION IOn a coordinate plane Mitchell’s house is located at (--5,2). Liam’s house is located at a point that is a reflection of Mitchell’s house over the y-axis. What are the coordinates of Liam’s house? Use the coordinate plane to help you think about the problem.

CHALLENGE QUESTION IIWhat is the distance between Mitchell and Liam’s house? (Answer in units: for example "2 units")

CHALLENGE QUESTION IIIWhat would the coordinates of Mitchell’s house be if it was reflected over the x-axis?

CHALLENGE QUESTION IVWhat would the coordinates be if Mitchell's house was reflected over the origin? Note: this is what Mr. Randolph calls a "double reflection," where the point is reflected over the x-axis AND over the y-axis.

The coordinates of point B are

Point C has the same first coordinate as Point AThe second coordinate of Point C is 1/2 the second coordinate of Point BWhat are the coordinates of Point C?

Locate and label point C on the coordinate plane.

Write the coordinates for Point C [use format (x,y)]

Which statement(s) about John’s points are true?Select all that apply.

Graph and label each point on the coordinate plane.
A) (7, --5)
B) (4, 5)
C) (--3, --4)
D) (2, 0)
E) (--6, 7)

Point A is located at (-4, 9) on the coordinate plane. Point B is located at (--4, --7).
What is the distance between Point A and Point B? Your answer should be in units.

Use the information below to plot and label John’s fourth point.
Neither coordinate of John’s fourth point is negative.
The horizontal distance between John’s fourth point and one of his other points is 2.

The coordinates of two vertices (corners) of a rectangle are (3, 3) and (--5, 3). If the rectangle has a
perimeter (distance around the outside) of 30 units, what are the possible coordinates of its other two vertices?

CHALLENGE QUESTION I
On a coordinate plane Mitchell’s house is located at (--5,2). Liam’s house is located at a point that is a reflection of Mitchell’s house over the y-axis. What are the coordinates of Liam’s house? Use the coordinate plane to help you think about the problem.

CHALLENGE QUESTION II
What is the distance between Mitchell and Liam’s house? (Answer in units: for example "2 units")

CHALLENGE QUESTION III
What would the coordinates of Mitchell’s house be if it was reflected over the x-axis?

CHALLENGE QUESTION IV
What would the coordinates be if Mitchell's house was reflected over the origin? Note: this is what Mr. Randolph calls a "double reflection," where the point is reflected over the x-axis AND over the y-axis.

Graph and label each point on the coordinate plane.
A) (7, --5)
B) (4, 5)
C) (--3, --4)
D) (2, 0)
E) (--6, 7)

Point C has the same first coordinate as Point A
The second coordinate of Point C is 1/2 the second coordinate of Point B
What are the coordinates of Point C?

Point A is located at (-4, 9) on the coordinate plane. Point B is located at (--4, --7).
What is the distance between Point A and Point B? Your answer should be in units.

Use the information below to plot and label John’s fourth point.
Neither coordinate of John’s fourth point is negative.
The horizontal distance between John’s fourth point and one of his other points is 2.

Which statement(s) about John’s points are true?
Select all that apply.

The coordinates of two vertices (corners) of a rectangle are (3, 3) and (--5, 3). If the rectangle has a
perimeter (distance around the outside) of 30 units, what are the possible coordinates of its other two vertices?

CHALLENGE QUESTION I
On a coordinate plane Mitchell’s house is located at (--5,2). Liam’s house is located at a point that is a reflection of Mitchell’s house over the y-axis. What are the coordinates of Liam’s house? Use the coordinate plane to help you think about the problem.

CHALLENGE QUESTION II
What is the distance between Mitchell and Liam’s house? (Answer in units: for example "2 units")

CHALLENGE QUESTION III
What would the coordinates of Mitchell’s house be if it was reflected over the x-axis?

CHALLENGE QUESTION IV
What would the coordinates be if Mitchell's house was reflected over the origin? Note: this is what Mr. Randolph calls a "double reflection," where the point is reflected over the x-axis AND over the y-axis.

Point C has the same first coordinate as Point A
The second coordinate of Point C is 1/2 the second coordinate of Point B
What are the coordinates of Point C?

Which statement(s) about John’s points are true?
Select all that apply.