Da el nombre de una figura geométrica que tenga las siguientes características:
1
Question 6
6.
Un tipo de cuadrilátero sin ejes de simetría.
1
Question 7
7.
Tipo de cuadrilátero cuyas diagonales son sus únicos ejes de simetría.
1
Relaciona atributos de cuadriláteros especiales con la simetría.
¿Qué más podría ser cierto acerca de los paralelogramos, rectángulos, cuadrados o rombos además de las características dadas sobre ellos en sus definiciones?
¿Cómo puedo estar convencido de que ciertas características deben ocurrir en cada miembro de una clase especial de cuadriláteros?
Hemos encontrado que muchos cuadriláteros diferentes poseen ejes de simetría y/o simetría rotacional. En el siguiente cuadro, escribe los nombres de los cuadriláteros que se describen en términos de sus simetrías.
Con base en las simetrías que hemos observado en varios tipos de cuadriláteros, podemos hacer afirmaciones sobre otras características y propiedades que pueden poseer los cuadriláteros.
Use the chart completed for Takeaways from Lesson 1.5 to complete this chart.
Use el cuadro completado para Conclusiones de la Lección 1.5 para completar este cuadro.
1
1
1
1
1
Question 13
13.
¿Por qué podría ser útil clasificar los cuadriláteros en términos de sus tipos de simetría, en lugar de en términos de sus características definitorias?
1
Question 14
14.
Share your answer with your pinky partner. Write down what your partner shared.
Comparte tu respuesta con tu compañero meñique. Anota lo que compartió tu pareja.
1
Question 15
15.
In your group, share out responses and write down ideas that are in common.
En su grupo, comparta las respuestas y escriba las ideas que tienen en común.
1
Question 16
16.
Un rectángulo es un cuadrilátero que contiene cuatro ángulos rectos.
Con base en lo que sabes sobre las transformaciones, ¿qué más podemos decir sobre los rectángulos además de la propiedad definitoria de que “los cuatro ángulos son ángulos rectos”? Haz una lista de propiedades adicionales de los rectángulos que parecen ser verdaderas (llamamos a tales declaraciones conjeturas) con base en la(s) transformación(es) del rectángulo sobre sí mismo. Querrás considerar las propiedades de los lados, los ángulos y las diagonales. Luego justifica por qué las propiedades serían verdaderas para este ejemplo específico de un rectángulo usando simetría transformacional.
1
Question 17
17.
Un paralelogramo es un cuadrilátero en el que los lados opuestos son paralelos.
Con base en lo que sabe sobre las transformaciones, ¿qué más podemos decir sobre los paralelogramos además de la propiedad definitoria de que “los lados opuestos de un paralelogramo son paralelos”? Haz una lista de propiedades adicionales de los paralelogramos que parezcan verdaderas según la(s) transformación(es) del paralelogramo sobre sí mismo. Querrás considerar las propiedades de los lados, ángulos y diagonales. Luego justifica por qué las propiedades serían verdaderas para este ejemplo específico de un paralelogramo usando simetría transformacional.
1
Question 18
18.
¿Qué características de los lados, ángulos y diagonales de un paralelogramo son iguales a las características de un rectángulo y qué características son diferentes?
¿Por qué es así?
1
Question 19
19.
Un rombo es un cuadrilátero en el que los cuatro lados son congruentes.
Con base en lo que sabes sobre las transformaciones, ¿qué más podemos decir sobre un rombo además de la propiedad definitoria de que "todos los lados son congruentes"? Haz una lista de propiedades adicionales de los rombos que parezcan verdaderas según la(s) transformación(es) del rombo sobre sí mismo. Querrás considerar las propiedades de los lados, ángulos y diagonales. Luego justifica por qué las propiedades serían verdaderas para este ejemplo específico de un rombo usando simetría transformacional.
1
Question 20
20.
Un cuadrado es a la vez un rectángulo y un rombo.
Con base en lo que sabes sobre transformaciones, ¿qué podemos decir sobre un cuadrado? Haz una lista de las propiedades de los cuadrados que parecen ser verdaderas según la(s) transformación(es) de los cuadrados sobre sí mismos. Querrás considerar las propiedades de los lados, ángulos y diagonales. Luego justifica por qué las propiedades serían verdaderas para este ejemplo específico de un cuadrado usando simetría transformacional.
1
Question 21
21.
Un trapezoide isósceles es un cuadrilátero con un par de lados paralelos y los lados no paralelos son congruentes, como se muestra en la figura ABCD. ¿Puedes encontrar una manera de demostrar que las siguientes afirmaciones son verdaderas?
Las diagonales no se bisecan entre sí.
Las diagonales son congruentes.
Los ángulos BAD y CBA son suplementarios, es decir, la medida del ángulo BAD más la medida del ángulo CBA es igual a 180 grados.
Nuestras conjeturas sobre las propiedades de los cuadriláteros (basadas en experimentación y razonamiento con transformaciones rígidas)
En el siguiente cuadro, escribe los nombres de los cuadriláteros que se describen en términos de sus características y propiedades, y luego registra cualquier característica o propiedad adicional de ese tipo de cuadrilátero que hayas observado. Esté preparado para compartir las razones de sus observaciones.
1
1
1
1
1
1
1
1
1
Question 30
30.
¿Qué notas acerca de las relaciones entre los cuadriláteros según sus características y la estructura del cuadro anterior?
1
Question 31
31.
¿Cómo se relacionan los gráficos al principio y al final de esta tarea? ¿Qué sugieren?
Lesson Summary
Muhtasari wa Somo
Resumen de la lección
Incamake y'Isomo
Soo koobid Cashar
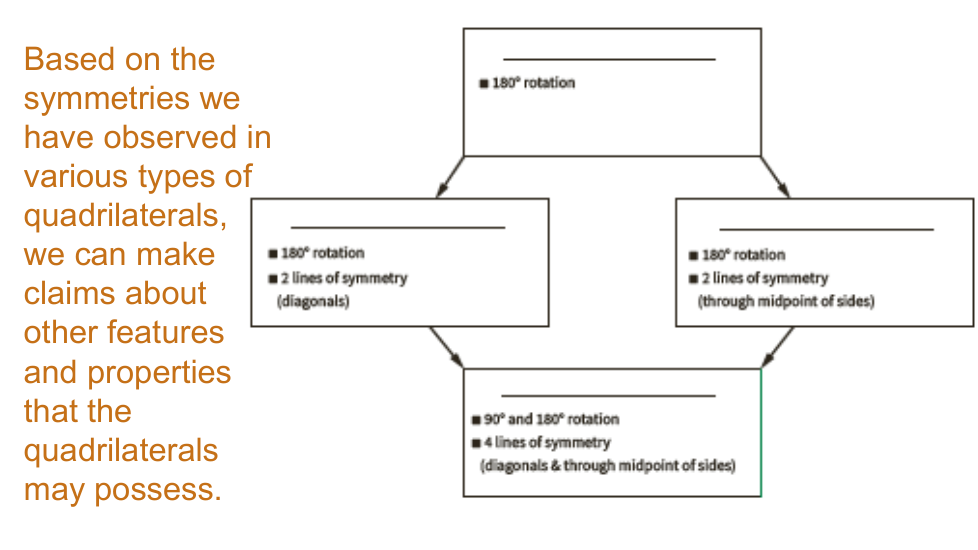
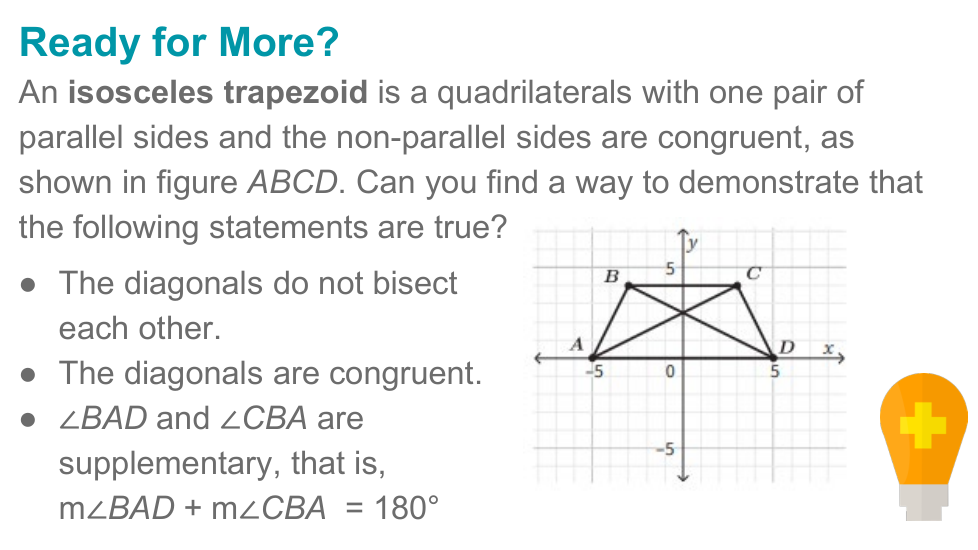
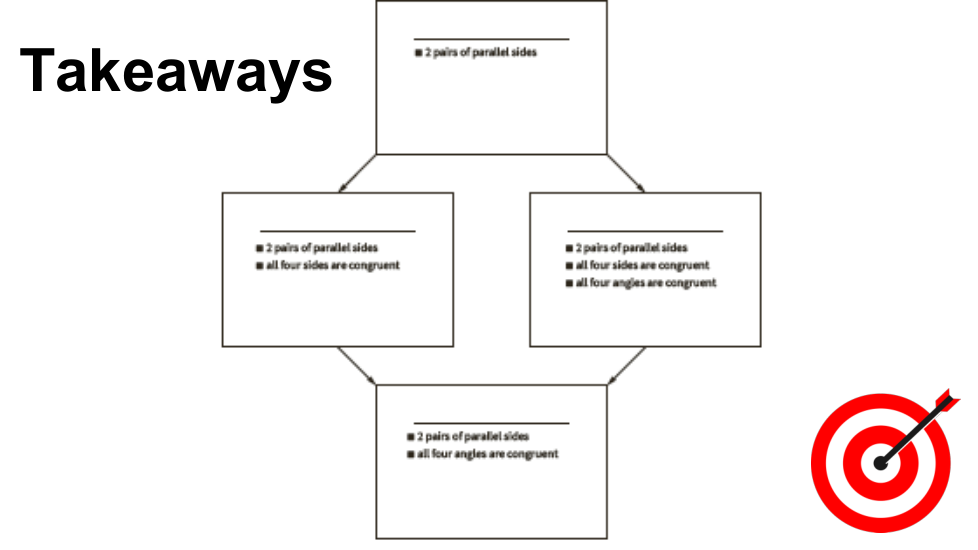
In this lesson, we used rigid transformations to examine properties of the sides, angles, and diagonals in parallelograms, rectangles, rhombuses, and squares. We learned that some quadrilaterals can be classified in terms of the properties they share with other quadrilaterals, such as congruent opposite sides or angles.
En esta lección, usamos transformaciones rígidas para examinar las propiedades de los lados, ángulos y diagonales en paralelogramos, rectángulos, rombos y cuadrados. Aprendimos que algunos cuadriláteros se pueden clasificar en términos de las propiedades que comparten con otros cuadriláteros, como lados opuestos o ángulos congruentes.
1
Question 32
32.
Explica cómo sabes que las diagonales de un rectángulo son congruentes.
Practice
Practica
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Standard 1A
I can accurately interpret/construct a geometric diagram to determine or represent geometric relationships.
Puedo interpretar/construir con precisión un diagrama geométrico para determinar o representar relaciones geométricas.
