Log inSign up for FREE
Library

U1 L2: Is It Right?

Last updated over 3 years ago
93 questions
Note from the author:
Open Up Resources

¿Qué es SEL?

ENSEÑANDO HABILIDADES DEL MUNDO REAL A LOS ESTUDIANTES

Autogestión
Conciencia de sí mismo
Conciencia social
Habilidades de comunicación/interpersonales
Toma de decisiones responsable


Haciendo del mundo un mejor lugar para estar, un salón de clases a la vez.

SEL ni iki?

KWIGISHA ABANYESHURI NYAKURI KOKO

Kwiyobora
Kumenya
Kumenyekanisha imibereho
Itumanaho / Ubuhanga bwa muntu
Gufata ibyemezo


Guhindura isi ahantu heza ho kuba, icyumba kimwe icyarimwe.

SEL ni nini?

WANAFUNZI WA KUFUNDISHA STADI HALISI ZA ULIMWENGU

Kujisimamia
Kujitambua
Uelewa wa Jamii
Ujuzi wa Mawasiliano/Binafsi
Uamuzi wa Kuwajibika


Kuifanya dunia kuwa mahali pazuri pa kuwa, darasa moja kwa wakati

QUE HACER CUANDO NO PUEDE DEJAR DE ESTRESARSE...

¡¡NO HAGAS ESPIRAL!!

Pruebe una de estas 5 formas saludables de relajar su cerebro.

  • NOMBRE TODOS LOS COLORES QUE PUEDA VER.​
  • IDENTIFIQUE LA EMOCIÓN Y DIARIO PRIVADO SOBRE ELLA.​
  • TRATA DE APRENDER ALGO NUEVO (UNA HABILIDAD O ACTIVIDAD FÍSICA)​
  • TRAZA TU MANO Y RESPIRA HACIA TU OMBLIGO
  • COMBATE CUALQUIER PENSAMIENTO NEGATIVO CON EL PENSAMIENTO POSITIVO EXACTAMENTE OPUESTO (EN VOZ ALTA SI ES POSIBLE)

ICYO GUKORA IYO UTASHOBORA GUHAGARIKA ...

NTIMUKORE UMWUKA !!


Gerageza bumwe muri ubu buryo 5 buzira umuze bwo gukuramo ubwonko bwawe.

  • IZINA NK'AMABARA MENSHI USHOBORA KUBONA.
  • KUMENYA AMARIMO N'IKINYAMAKURU CYANE KUBYEREKEYE.
  • GERAGEZA KUMENYA BINTU BISHYA (IGIKORWA CYANGWA UMURIMO)
  • SHAKA UKUBOKO KWE KANDI UHUME MURI BUTTON YANYU
  • URWANYA ICYITEKEREZO CYOSE GITEKEREZO KUBITEKEREZO BYIZA BITEKEREZO (HANZE NIBA BISHOBOKA)

NINI UFANYE UNAPOSHINDWA KUACHA KUStress...

USICHOKE!!


Jaribu mojawapo ya njia hizi 5 zenye afya za kuburudisha ubongo wako

  • TAJA RANGI NYINGI UNAZOWEZA KUONA
  • TAMBUA HISIA NA JARIDA FARAGHA KUHUSU HILO...
  • JARIBU KUJIFUNZA JAMBO JIPYA (UJUZI AU ZOEZI LA MWILI)
  • ZINGATIA MKONO NA PUMZI YAKO NDANI YA KITUFE CHA TUMBO
  • PAMBANA NA MAWAZO YOYOTE HASI KWA WAZO CHANYA NYINGINE HASA (KWA MAkelele, IKIWEZEKANA)​

IF YOU WERE BAD ABOUT​ MATH, THAT IS IN THE PAST​... THAT IS OKAY!

YOU ARE ALLOWED TO MAKE MISTAKES
Learn and grow from them.

Let's take a deep breath in, and breath out for a count of 5, 4, 3, 2, 1 and let it go.

SI ERAS MALO EN MATEMÁTICAS, ESO ESTÁ EN EL PASADO... ¡ESTÁ BIEN!

TIENES PERMISO PARA COMETIR ERRORES
Aprende y crece a partir de ellos.

Inhalemos profundamente y exhalemos contando hasta 5, 4, 3, 2, 1 y soltémoslo.

NIBA WARI MUBYI MATA, IYI KERA ... NIBYIZA!

UREMEREWE GUKORA AMAKOSA
Iga kandi ukure muri bo.

Reka duhumeke neza, hanyuma duhumeke kubara 5, 4, 3, 2, 1 hanyuma tubireke.

IKIWA ULIKUWA MBAYA KUHUSU HISABATI, HAPO HAPO NYUMA... NI SAWA!

UNARUHUSIWA KUFANYA MAKOSA
Jifunze na ukue kutoka kwao.

Wacha tuvute pumzi ndani, na tupumue nje kwa hesabu ya 5, 4, 3, 2, 1 na tuiruhusu iende.
Hoy es un nuevo día con una nueva oportunidad de hacer de tu mundo un mejor lugar para estar.
Uyu munsi numunsi mushya ufite amahirwe mashya yo guhindura isi yawe ahantu heza ho kuba.
Leo ni siku mpya yenye fursa mpya ya kufanya ulimwengu wako kuwa mahali pazuri pa kuwa.

Donuts Check In

Kugenzura Amafaranga

Donuts Ingia


0
Which Donut are you?
Donut kee baad tahay?
Wewe ni Donut gani?
Ninde Donut?
¿Qué Donut eres?
__________
0

What is today's date?

¿Cuál es la fecha de hoy?

Itariki yuyu munsi niyihe?

Tarehe ya leo ni nini?

0

What is the title of the lesson you will be working on today?

¿Cuál es el título de la lección en la que trabajará hoy?

Nuwuhe mutwe w'isomo uzakora uyu munsi?

Je, kichwa cha somo litakalofanyia kazi leo ni kipi?

0

Any other information I need to know to help you be successful today?

¿Alguna otra información que necesite saber para ayudarlo a tener éxito hoy?

Andi makuru yose nkeneye kumenya kugirango agufashe gutsinda uyu munsi?

Taarifa nyingine yoyote ninayohitaji kujua ili kukusaidia kufanikiwa leo?

1B

I can accurately interpret geometric relationships to set up a symbolic representation and determine an unknown quantity.

Puedo interpretar con precisión las relaciones geométricas para establecer una representación simbólica y determinar una cantidad desconocida.

Nshobora gusobanura neza isano ya geometrike kugirango nshyireho ikimenyetso cyikigereranyo kandi menye umubare utazwi.

Success Criteria:

I can accurately identify the type of function or formula needed.
I CAN USE CORRECT UNITS OF MEASURE
I CAN USE CORRECT TERMINOLOGY
I can accurately place coefficients, exponents & constraints in a given equation OR FORMULA format

Criterios de éxito:

Puedo identificar con precisión el tipo de función o fórmula necesaria.
PUEDO USAR LAS UNIDADES DE MEDIDA CORRECTAS
PUEDO UTILIZAR LA TERMINOLOGÍA CORRECTA
Puedo colocar con precisión coeficientes, exponentes y restricciones en una ecuación determinada O formato de FÓRMULA

Ibipimo byo gutsinda:

Nshobora kumenya neza ubwoko bwimikorere cyangwa formula ikenewe.
NASHOBORA GUKORESHA UNITS ZIKURIKIRA
NASHOBORA GUKORESHA TERMINOLOGIYA
Nshobora gushyira neza coefficient, ibyerekana & imbogamizi muburyo bwatanzwe CYANGWA FORMULA
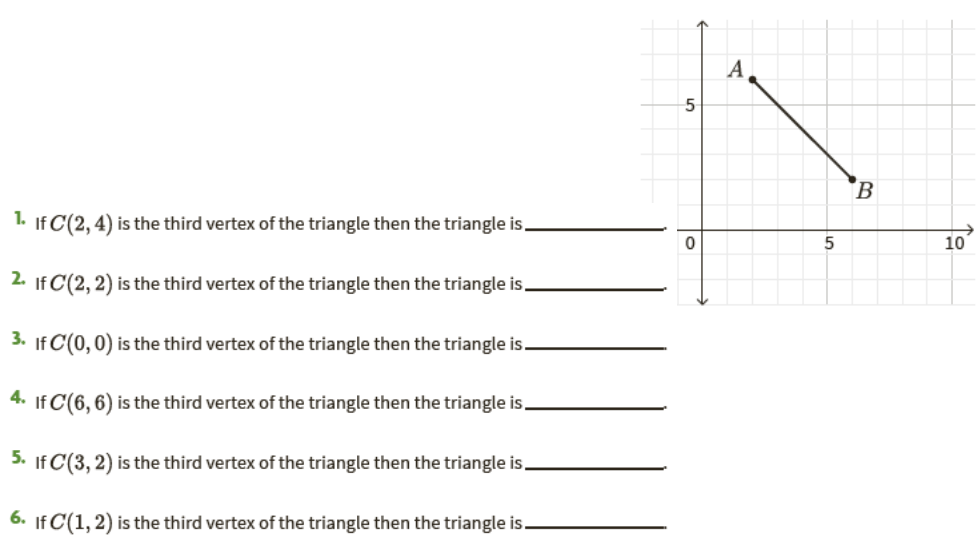
El segmento de línea dado en la cuadrícula de coordenadas, con extremos en A(2, 6) y B(6, 2), es un lado de un triángulo. Describe el triángulo formado si cada uno de los siguientes puntos es el tercer vértice C del triángulo. (Use palabras en su descripción como agudo, obtuso, recto, escaleno, isósceles, equilátero).
1
If C(2,4) is the third vertex of the triangle then the triangle is
Si C(2,4) es el tercer vértice del triángulo, entonces el triángulo es
__________ & __________
1
If C(2,2) is the third vertex of the triangle then the triangle is
Si C(2,2) es el tercer vértice del triángulo, entonces el triángulo es
__________ & __________
1
If C(0, 0) is the third vertex of the triangle then the triangle is
Si C(0, 0) es el tercer vértice del triángulo, entonces el triángulo es
__________ & __________
1
If C(6, 6) is the third vertex of the triangle then the triangle is
Si C(6, 6) es el tercer vértice del triángulo, entonces el triángulo es
__________ & __________
1
If C(3, 2) is the third vertex of the triangle then the triangle is
Si C(3, 2) es el tercer vértice del triángulo, entonces el triángulo es
__________ & __________
1
If C(1, 2) is the third vertex of the triangle then the triangle is
Si C(1, 2) es el tercer vértice del triángulo, entonces el triángulo es
__________ & __________
Reconocer rectas paralelas y perpendiculares en un plano coordenado.
1

¿Cómo puedo determinar si dos líneas en un plano de coordenadas son paralelas o perpendiculares? ¿Es suficiente el examen visual (es decir, “Parece”)?

En Leaping Lizards, probablemente pensaste mucho en las líneas paralelas y perpendiculares, particularmente cuando trasladaste los puntos de anclaje del lagarto a la misma distancia y en la misma dirección, o giraste el lagarto alrededor de un centro dado a través de un ángulo, o reflejaste el lagarto a través de una línea. Sería útil poder predecir cuándo las líneas en una cuadrícula de coordenadas son paralelas o perpendiculares entre sí.
Examina el siguiente diagrama y escribe declaraciones para describir qué líneas son paralelas entre sí.
1

My list of parallel lines:
Use // to show parallel lines. Example AB // XZ means line AB is parallel to line XZ.

Mi lista de lineas paralelas:
Use // para mostrar líneas paralelas. Ejemplo AB // XZ significa que la línea AB es paralela a la línea XZ.

1

¿Cómo supiste que estas líneas eran paralelas, además de “Parecen líneas paralelas”?

Es posible que hayas escrito tus afirmaciones sobre líneas paralelas usando palabras como: "La línea que pasa por los puntos A y B es paralela a la línea que pasa por los puntos G y H". Podemos enunciar esta misma idea simbólicamente.

Retrieval

Recuperación

Kubona

Urejeshaji

1

Use the coordinate grid to find the length of each side of the triangle.

Usa la cuadrícula de coordenadas para encontrar la longitud de cada lado del triángulo.


Solve each equation for the indicated variable.
Resuelve cada ecuación para la variable indicada.
1

Solve for x.

1

Solve for y.

0

How are you doing today?
¿Cómo estás hoy?

Review your notes from yesterday. Write down any questions or AHA moments you have on the whiteboard for #13.
Revisa tus notas de ayer. Escriba cualquier pregunta o momento AHA que tenga en la pizarra para el n.º 13.
1

¿Cómo se conecta esta definición con las ideas sobre las líneas perpendiculares, como "las líneas perpendiculares se encuentran en ángulo recto"?

1

¿Cómo podríamos demostrar esta definición usando las transformaciones que exploramos en Leaping Lizards?

1

Using your answers from 18 & 19, come up with a short paragraph that answers both questions with your partner.

Usando sus respuestas de 18 y 19, elabore un breve párrafo que responda a ambas preguntas con su compañero.

Ahora que hemos hecho una observación sobre las pendientes de las líneas paralelas, será útil hacer una observación sobre las pendientes de las líneas perpendiculares. Quizás en Leaping Lizards usaste un transportador o alguna otra herramienta o estrategia para ayudarte a formar un ángulo recto. En esta tarea, consideramos cómo crear un ángulo recto prestando atención a las pendientes en la cuadrícula de coordenadas.
Comenzamos enunciando una idea fundamental para nuestro trabajo: Las líneas horizontales y verticales son perpendiculares. Por ejemplo, en una cuadrícula de coordenadas, la línea horizontal y=2 y la línea vertical x=3 se intersecan para formar cuatro ángulos rectos.

Pero, ¿y si una línea o un segmento de línea no es horizontal ni vertical? ¿Cómo determinamos la pendiente de una recta o segmento de recta que será perpendicular a ella?
0

Notes
notas

0

Notes
notas

0

Notes
notas

0

Notes
notas

1

What is the slope of the line segment when you consider the points A(2, 3) and B(4, 7) and the line segment
¿Cuál es la pendiente del segmento de recta cuando consideras los puntos A(2, 3) y B(4, 7) y el segmento de recta

1

Locate and name a third point C(x, y) on the coordinate grid, so the points A(2, 3), B(4, 7) and C(x, y) form the vertices of a right triangle, with a hypotenuse of
Localiza y nombra un tercer punto C(x, y) en la cuadrícula de coordenadas, de modo que los puntos A(2, 3), B(4, 7) y C(x, y) formen los vértices de un triángulo rectángulo, con un hipotenusa de

1

Explain how you know that the triangle you formed contains a right angle.

Explica cómo sabes que el triángulo que formaste contiene un ángulo recto.

1

Now rotate this right triangle 90o about the vertex point A(2, 3). Explain how you know that your have rotated the triangle 90o.

Ahora rota este triángulo rectángulo 90o sobre el punto de vértice A(2, 3). Explica cómo sabes que has rotado el triángulo 90o.

1

Compare the slope of the hypotenuse of this rotated right triangle with the slope of the hypotenuse of the pre-image. What do you notice?

Compara la pendiente de la hipotenusa de este triángulo rectángulo rotado con la pendiente de la hipotenusa de la imagen previa. ¿Que notaste?

1

What is the slope of the line segment when you consider the points A(2, 3) and B(5, 4) and the line segment
¿Cuál es la pendiente del segmento de recta cuando consideras los puntos A(2, 3) y B(5, 4) y el segmento de recta

1

Locate and name a third point C(x, y) on the coordinate grid, so the points A(2, 3), B(5, 4) and C(x, y) form the vertices of a right triangle, with
Localiza y nombra un tercer punto C(x, y) en la cuadrícula de coordenadas, de modo que los puntos A(2, 3), B(5,4) y C(x, y) formen los vértices de un triángulo rectángulo, con un hipotenusa de

1

Explain how you know that the triangle you formed contains a right angle.

Explica cómo sabes que el triángulo que formaste contiene un ángulo recto.

1

Now rotate this right triangle 90o about the vertex point A(2, 3). Explain how you know that your have rotated the triangle 90o.

Ahora rota este triángulo rectángulo 90o sobre el punto de vértice A(2, 3). Explica cómo sabes que has rotado el triángulo 90o.

1

Compare the slope of the hypotenuse of this rotated right triangle with the slope of the hypotenuse of the pre-image. What do you notice?

Compara la pendiente de la hipotenusa de este triángulo rectángulo rotado con la pendiente de la hipotenusa de la imagen previa. ¿Que notaste?

1

What is the slope of the line segment when you consider the points A(2, 3) and B(7, 5) and the line segment
¿Cuál es la pendiente del segmento de recta cuando consideras los puntos A(2, 3) y B(7, 5) y el segmento de recta

1

Locate and name a third point C(x, y) on the coordinate grid, so the points A(2, 3), B(7, 5) and C(x, y) form the vertices of a right triangle, with
Localiza y nombra un tercer punto C(x, y) en la cuadrícula de coordenadas, de modo que los puntos A(2, 3), B(7, 5) y C(x, y) formen los vértices de un triángulo rectángulo, con un hipotenusa de

1

Explain how you know that the triangle you formed contains a right angle.

Explica cómo sabes que el triángulo que formaste contiene un ángulo recto.

1

Now rotate this right triangle 90o about the vertex point A(2, 3). Explain how you know that your have rotated the triangle 90o.

Ahora rota este triángulo rectángulo 90o sobre el punto de vértice A(2, 3). Explica cómo sabes que has rotado el triángulo 90o.

1

Compare the slope of the hypotenuse of this rotated right triangle with the slope of the hypotenuse of the pre-image. What do you notice?

Compara la pendiente de la hipotenusa de este triángulo rectángulo rotado con la pendiente de la hipotenusa de la imagen previa. ¿Que notaste?

1

What is the slope of the line segment when you consider the points A(2, 3) and B(0, 6) and the line segment
¿Cuál es la pendiente del segmento de recta cuando consideras los puntos A(2, 3) y B(0, 6) y el segmento de recta

1

Locate and name a third point C(x, y) on the coordinate grid, so the points A(2, 3), B(0, 6) and C(x, y) form the vertices of a right triangle, with
Localiza y nombra un tercer punto C(x, y) en la cuadrícula de coordenadas, de modo que los puntos A(2, 3), B(0, 6) y C(x, y) formen los vértices de un triángulo rectángulo, con un hipotenusa de

1

Explain how you know that the triangle you formed contains a right angle.

Explica cómo sabes que el triángulo que formaste contiene un ángulo recto.

1

Now rotate this right triangle 90o about the vertex point A(2, 3). Explain how you know that your have rotated the triangle 90o.

Ahora rota este triángulo rectángulo 90o sobre el punto de vértice A(2, 3). Explica cómo sabes que has rotado el triángulo 90o.

1

Compare the slope of the hypotenuse of this rotated right triangle with the slope of the hypotenuse of the pre-image. What do you notice?

Compara la pendiente de la hipotenusa de este triángulo rectángulo rotado con la pendiente de la hipotenusa de la imagen previa. ¿Que notaste?

1

Based on experiments 1–4, state an observation about the slopes of perpendicular lines.

While this observation is based on a few specific examples, can you create an argument or justification for why this is always true?


Con base en los experimentos 1 a 4, establezca una observación sobre las pendientes de las líneas perpendiculares.

Si bien esta observación se basa en algunos ejemplos específicos, ¿puede crear un argumento o una justificación de por qué esto siempre es cierto?

Now that we know how to identify perpendicular lines on a coordinate grid, we can also use symbolic notation to indicate that the two lines are perpendicular.
Now that we know how to identify perpendicular lines on a coordinate grid, we can also use symbolic notation to indicate that the two lines are perpendicular.

Criticar, corregir y aclarar:


Mire cuidadosamente las palabras y los diagramas. ¿Tienen sentido?

¿Vemos un error que necesita ser corregido?

¿Dejamos algo fuera que necesita ser puesto?

¿Sabemos algo más que deba agregarse?

¿Por qué queremos hacer los cambios que estamos proponiendo?
1

Para los experimentos 1 a 4, escribe las ecuaciones de las rectas que contienen la hipotenusa del triángulo original y la hipotenusa del triángulo rotado tanto en la forma punto-pendiente como en la forma pendiente-intersección, usando el punto en el centro de rotación para el punto -pendiente forma de la ecuación. ¿Qué relaciones notas en estas ecuaciones?

Al trabajar con líneas en una cuadrícula de coordenadas,
1

I know the lines are parallel if
Sé que las rectas son paralelas si

1

I know the lines are perpendicular if
Sé que las rectas son perpendiculares si

1

I can indicate two lines are parallel using the following notation:
Puedo indicar que dos líneas son paralelas usando la siguiente notación:

In representing parallel lines on a coordinate grid, we have drawn images to represent the following undefined terms: point, line, and plane. These are abstract ideas, rather than concrete objects because:
Al representar líneas paralelas en una cuadrícula de coordenadas, hemos dibujado imágenes para representar los siguientes términos indefinidos: punto, línea y plano. Estas son ideas abstractas, en lugar de objetos concretos porque:
1

Unlike a dot, a point
A diferencia de un punto, un punto

1

Unlike a straight stroke of ink, a line
A diferencia de un trazo recto de tinta, una línea

1

Unlike a piece of paper, a plane
A diferencia de una hoja de papel, un avión

Vocabulary

amagambo

maneno ya msamiati

Palabras de vocabulario

Erayada

Open Up HS Math | Geometry - Glossary (openupresources.org)
0

Pythagorean theorem
Teorema de pitágoras

0

acute angle
ángulo agudo

0

equilateral, equilateral triangle
equilátero, triángulo equilátero

0

isosceles triangle, trapezoid
triángulo isósceles, trapezoide

0

line
línea

0

line segment
segmento de línea

0

obtuse angle/obtuse triangle
ángulo obtuso/triángulo obtuso

0

plane
plana

0

point
punto

0

right angle
ángulo recto

0

scalene triangle
triángulo escaleno

Lesson Summary

Muhtasari wa Somo

Resumen de la lección

Incamake y'Isomo

Soo koobid Cashar

In this lesson, we learned criteria for determining if two lines in a coordinate plane are parallel or perpendicular. We also learned notation for indicating that lines are parallel or perpendicular in our written work.
En esta lección, aprendimos los criterios para determinar si dos líneas en un plano de coordenadas son paralelas o perpendiculares. También aprendimos la notación para indicar que las líneas son paralelas o perpendiculares en nuestro trabajo escrito.

Check for Understanding:

Angalia Uelewa:

Hubi Fahamka:

Reba kugirango ubyumve:

Verificar comprensión:

1

Write equations of two lines that would be parallel to each other when graphed on a coordinate grid.

Escribe ecuaciones de dos líneas que serían paralelas entre sí cuando se graficaran en una cuadrícula de coordenadas.

1

Write equations of two lines that would be perpendicular to each other when graphed on a coordinate grid.

Escribe ecuaciones de dos rectas que serían perpendiculares entre sí cuando se graficaran en una cuadrícula de coordenadas.

Practice

Practica


Calculator:
Calculadora:

https://www.desmos.com/scientific
Construction websites:
Sitios web de construcción:

https://www.geogebra.org/m/VQ57WNyR
Use the coordinate grid to find the length of each side of the triangles provided. Give answers in exact form.
Usa la cuadrícula de coordenadas para encontrar la longitud de cada lado de los triángulos provistos. Dar respuestas en forma exacta.
1

1

1

1

1

Graph a line parallel to the given line.
Grafica una recta paralela a la recta dada.

1

Equation for given line:
Ecuación para la recta dada:

1

Equation for new line:
Ecuación para nueva línea:

1

Graph a line parallel to the given line.
Grafica una recta paralela a la recta dada.

1

Equation for given line:
Ecuación para la recta dada:

1

Equation for new line:
Ecuación para nueva línea:

1

Graph a line parallel to the given line.
Grafica una recta paralela a la recta dada.

1

Equation for given line:
Ecuación para la recta dada:

1

Equation for new line:
Ecuación para nueva línea:

1

Graph a line perpendicular to the given line.
Grafica una recta perpendicular a la recta dada.

1

Equation for given line:
Ecuación para la recta dada:

1

Equation for new line:
Ecuación para nueva línea:

1

Graph a line perpendicular to the given line.
Grafica una recta perpendicular a la recta dada.

1

Equation for given line:
Ecuación para la recta dada:

1

Equation for new line:
Ecuación para nueva línea:

1

Graph a line perpendicular to the given line.
Grafica una recta perpendicular a la recta dada.

1

Equation for given line:
Ecuación para la recta dada:

1

Equation for new line:
Ecuación para nueva línea:

Solve each equation for the indicated variable.
Resuelve cada ecuación para la variable indicada.
1

Solve for x.

1

Solve for n.

1

Solve for x.

1

Solve for y.

Additional Resources

Ibikoresho by'inyongera

Rasilimali za Ziada

Recursos adicionales

Khayraad Dheeraad ah

Homework help and hints:

https://tinyurl.com/5xsazedw
Ayuda con la tarea y consejos:

https://tinyurl.com/534bpwhx

Standard 1B

I can accurately interpret geometric relationships to set up a symbolic representation and determine an unknown quantity.

Puedo interpretar con precisión las relaciones geométricas para establecer una representación simbólica y determinar una cantidad desconocida.

Nshobora gusobanura neza isano ya geometrike kugirango nshyireho ikimenyetso cyikigereranyo kandi menye umubare utazwi.


1

What score do you give yourself?

Ni ayahe manota wiha wenyine?

Dhibco noocee ah ayaad naftaada siisaa?

Unajipa alama gani?

¿Qué puntuación te das a ti mismo?

4

Cite your evidence from the assignment and explain how it supports your score.

Cite su evidencia de la tarea y explique cómo respalda su puntaje.

Taja ushahidi wako kutoka kwa kazi na ueleze jinsi inavyosaidia alama yako.

Soo qaado caddayntaada hawsha oo sharax sida ay u taageerto dhibcahaaga.

Tanga ibimenyetso byawe uhereye kumikoro hanyuma usobanure uburyo ishyigikira amanota yawe.