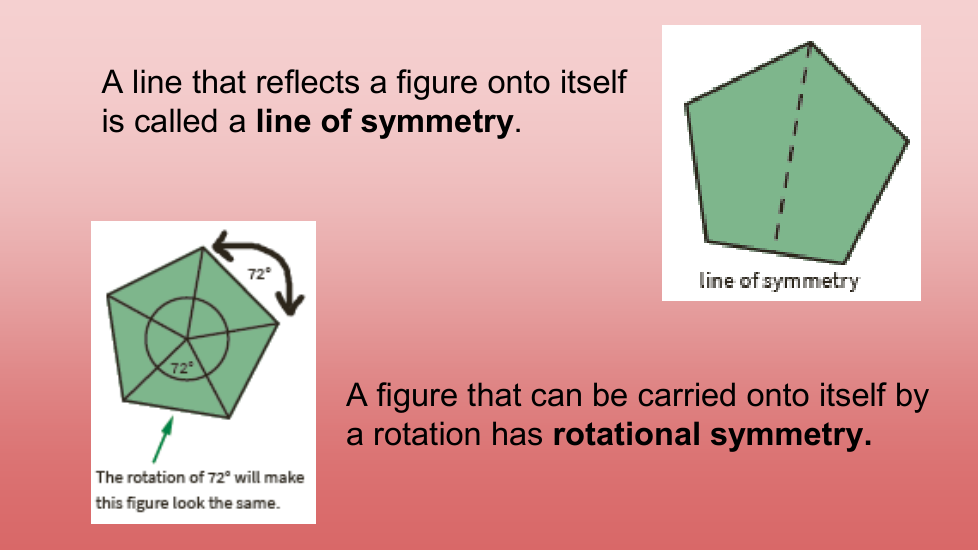
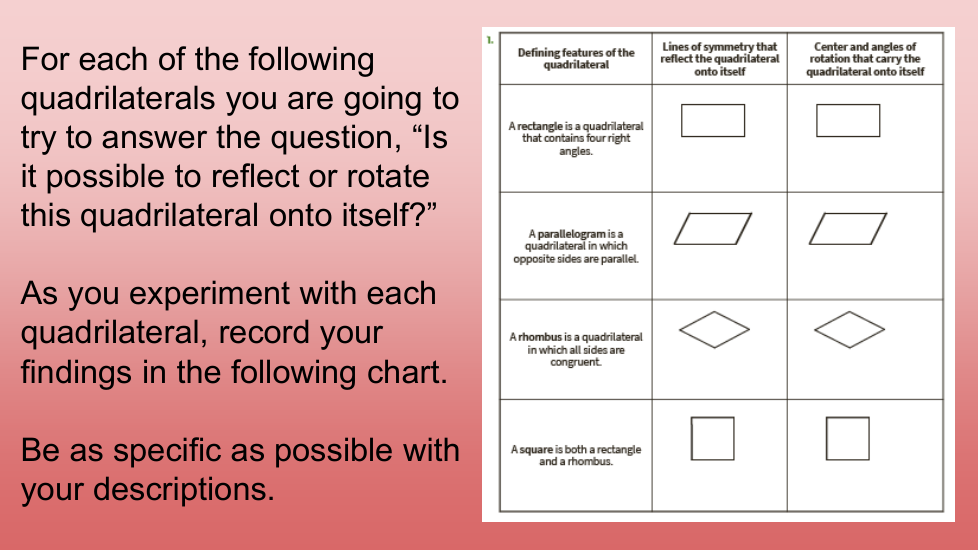
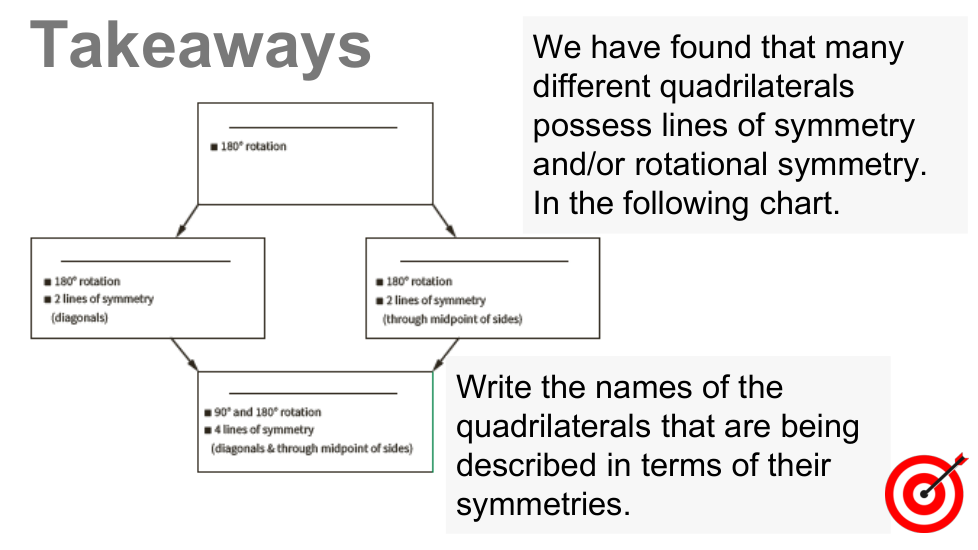
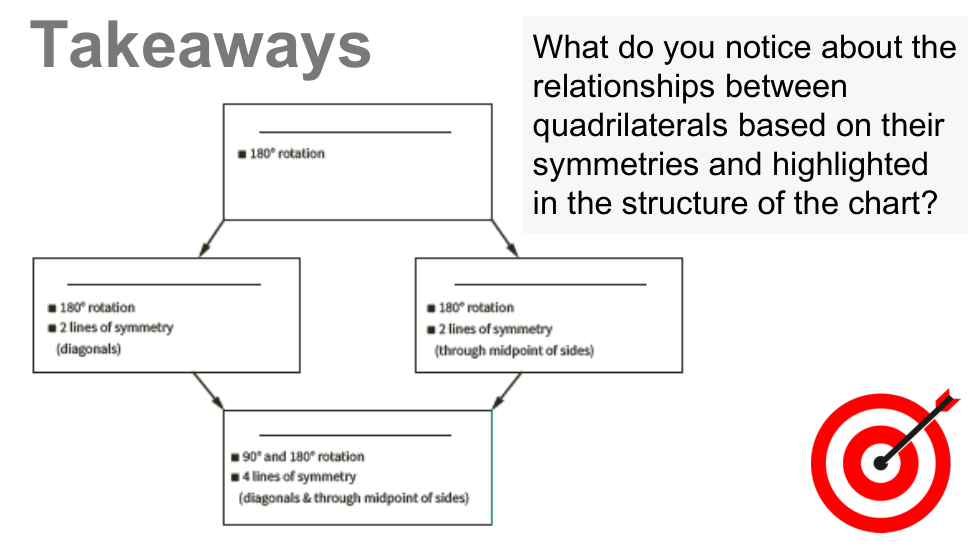
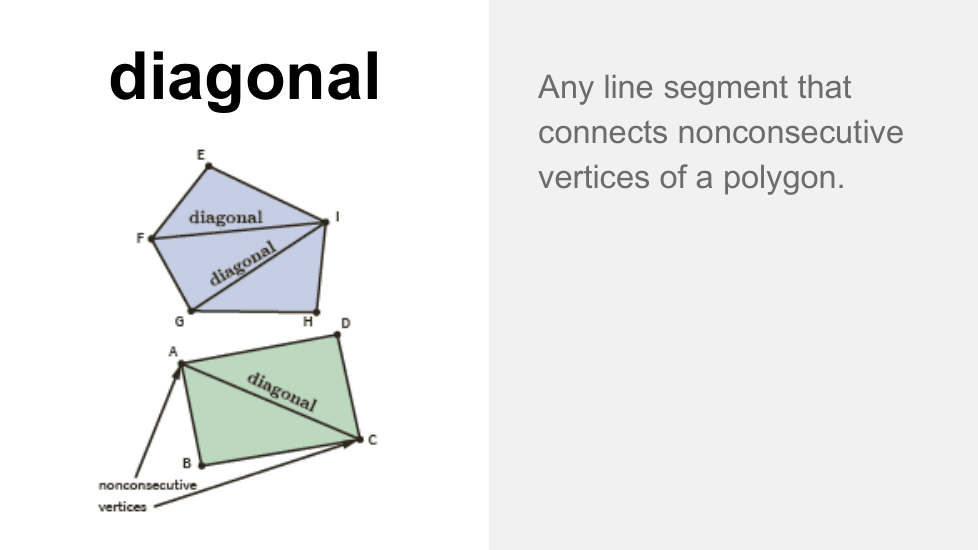
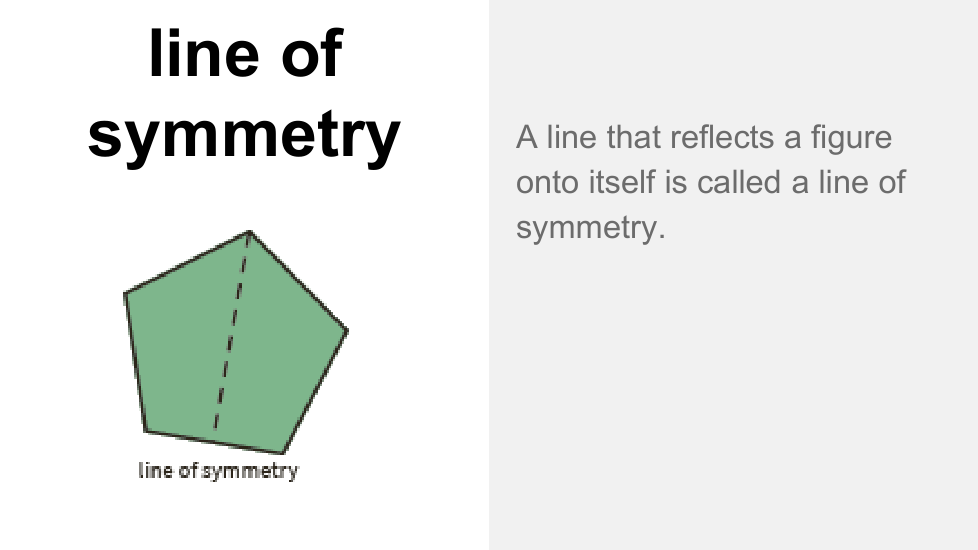
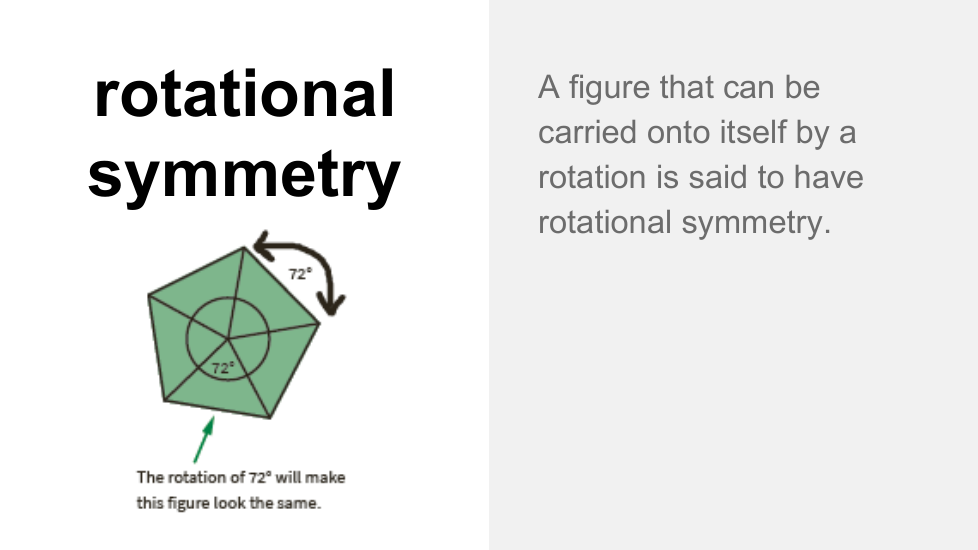
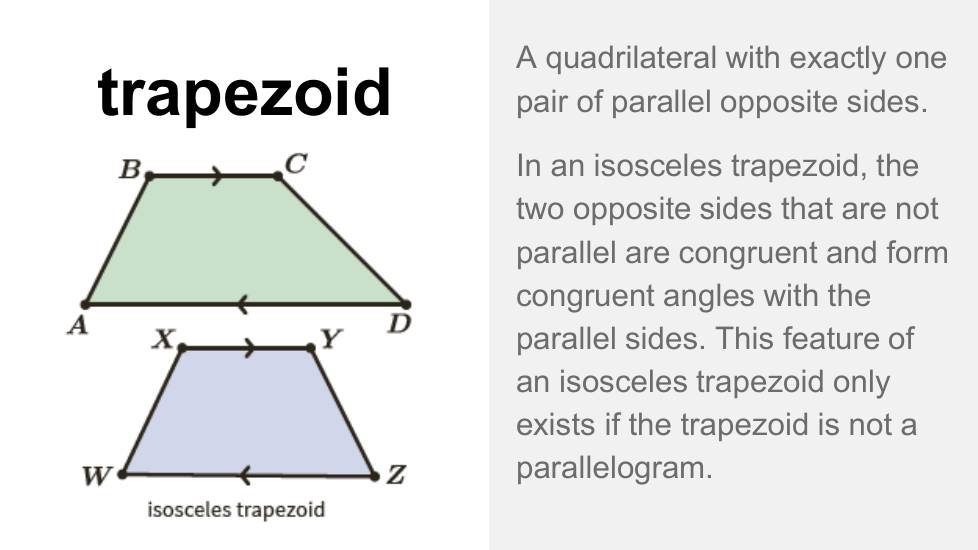
En esta lección, exploramos la simetría lineal y rotacional en diferentes tipos de cuadriláteros. Una figura es simétrica si una figura puede reflejarse a lo largo de una línea o rotar sobre sí misma alrededor de un punto. Encontramos que las diagonales y las líneas que conectan los puntos medios de los lados opuestos de un cuadrilátero pueden ser ejes de simetría, según el cuadrilátero, y el punto de intersección de las diagonales es el centro de rotación de paralelogramos, rectángulos, rombos y cuadrados. Los posibles ángulos de rotación varían según el cuadrilátero, pero siempre son múltiplos de 90o.