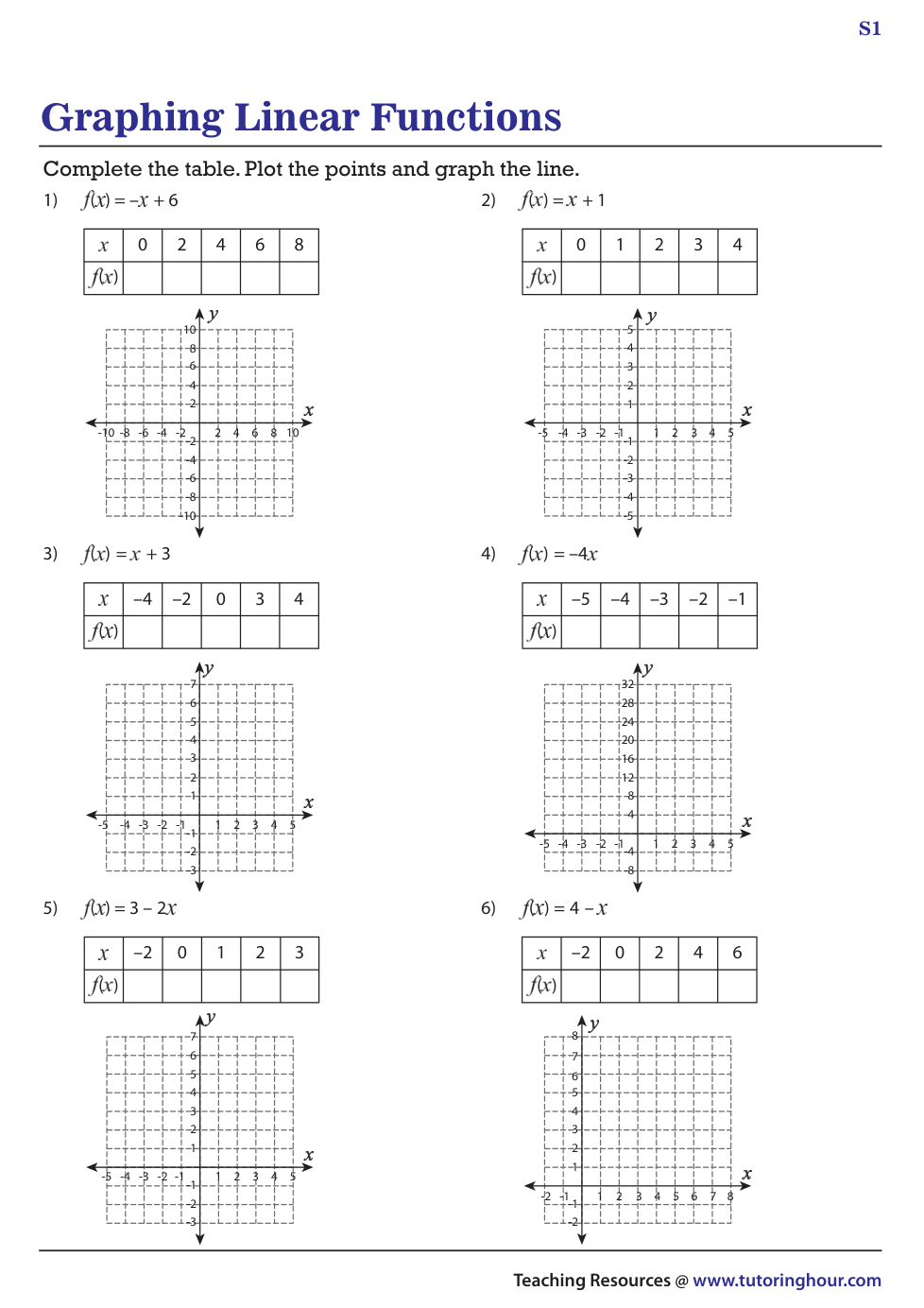
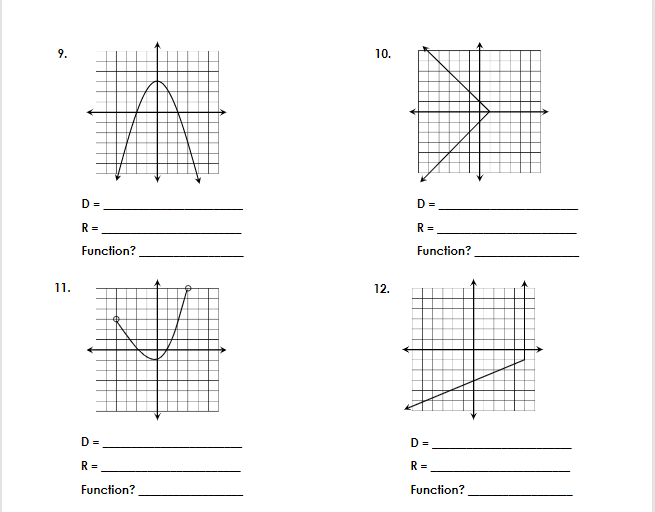
Formative 2: Function Equations and Continuous Domain/Range
star
star
star
star
star
Last updated over 1 year ago
13 questions
2
Complete the table by matching the x-value with the correct f(x)-value.f(x) = -x + 6(Level 2)
Complete the table by matching the x-value with the correct f(x)-value.
f(x) = -x + 6
(Level 2)
| Draggable item | arrow_right_alt | Corresponding Item |
|---|---|---|
x = 8 | arrow_right_alt | f(x) = 6 |
x = 0 | arrow_right_alt | f(x) = 4 |
x = 6 | arrow_right_alt | f(x) = 2 |
x = 2 | arrow_right_alt | f(x) = 0 |
x = 4 | arrow_right_alt | f(x) = -2 |
2
Graph the points from Question 1.(Level 2)
Graph the points from Question 1.
(Level 2)
- Click the graph tab.
- Click on the graph background to add a point. Add two points to create a graph. Drag a point or type in x and y coordinates to edit its position. Click on a point to delete it.
2
Complete the table by matching the x-value with the correct f(x)-value.f(x) = 3 - 2x(Level 2)
Complete the table by matching the x-value with the correct f(x)-value.
f(x) = 3 - 2x
(Level 2)
| Draggable item | arrow_right_alt | Corresponding Item |
|---|---|---|
x = 0 | arrow_right_alt | f(x) = 7 |
x = 3 | arrow_right_alt | f(x) = 3 |
x = 1 | arrow_right_alt | f(x) = 1 |
x = 2 | arrow_right_alt | f(x) = -1 |
x = -2 | arrow_right_alt | f(x) = -3 |
2
Graph the points from Question 3.(Level 2)
Graph the points from Question 3.
(Level 2)
- Click the graph tab.
- Click on the graph background to add a point. Add two points to create a graph. Drag a point or type in x and y coordinates to edit its position. Click on a point to delete it.
3
Given the function and domain, find the range values.y = -4x; domain = {-5, -4, -3, -2, -1}(Level 3)
Given the function and domain, find the range values.
y = -4x; domain = {-5, -4, -3, -2, -1}
(Level 3)
3
Given the function and domain, find the range values.y = 4 - x; domain = {-2, 0, 2, 4, 6}(Level 3)
Given the function and domain, find the range values.
y = 4 - x; domain = {-2, 0, 2, 4, 6}
(Level 3)
3
What is the domain?(Level 3)
What is the domain?
(Level 3)
3
What is the range?(Level 3)
What is the range?
(Level 3)
3
What is the domain?(Level 3)
What is the domain?
(Level 3)
3
What is the range?(Level 3)
What is the range?
(Level 3)
3
What is the domain?(Level 3)
What is the domain?
(Level 3)
3
What is the range?(Level 3)
What is the range?
(Level 3)
4
Explain why the range is all real numbers, but the domain isn't.(Level 4)
Explain why the range is all real numbers, but the domain isn't.
(Level 4)