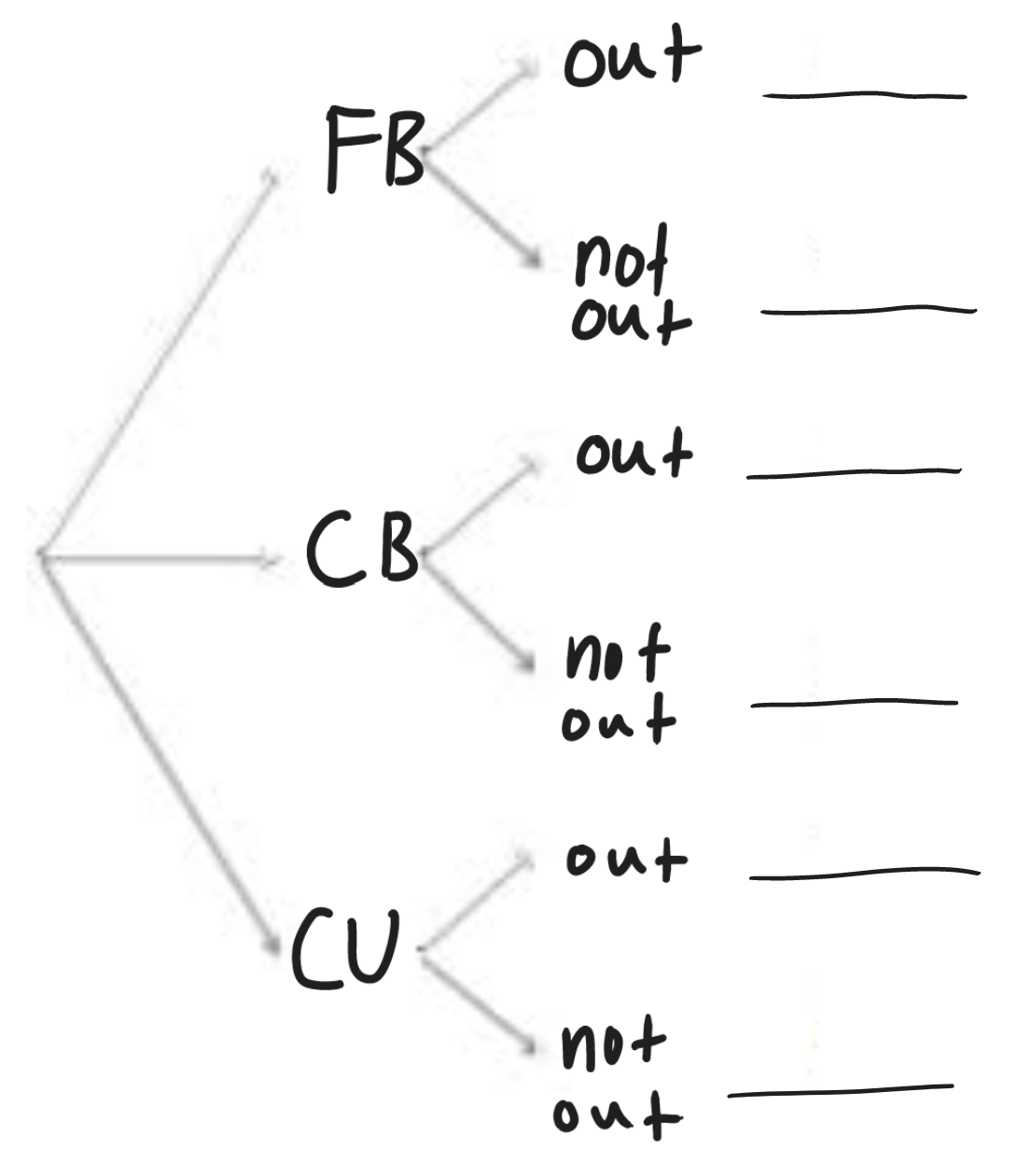
Many baseball pitchers can throw 3 different types of pitches: fastball, curve, and change-up. When facing a batter with only one strike left, a certain pitcher throws his fastball 45% of the time, curveball 35% of the time, and change-up the remaining times. The pitcher gets the batter out 75% of the time when he throws a fastball, 80% of the time when he throws a curveball, and 65% of the time when he throws a change-up. Randomly select one batter during a game.