Log inSign up for FREE
Library

6-1 First Day Interior Exterior Angle Sum

Last updated over 1 year ago
16 questions
You can skip to about the 11:15 minute mark in this video to get to where I am at on these notes.
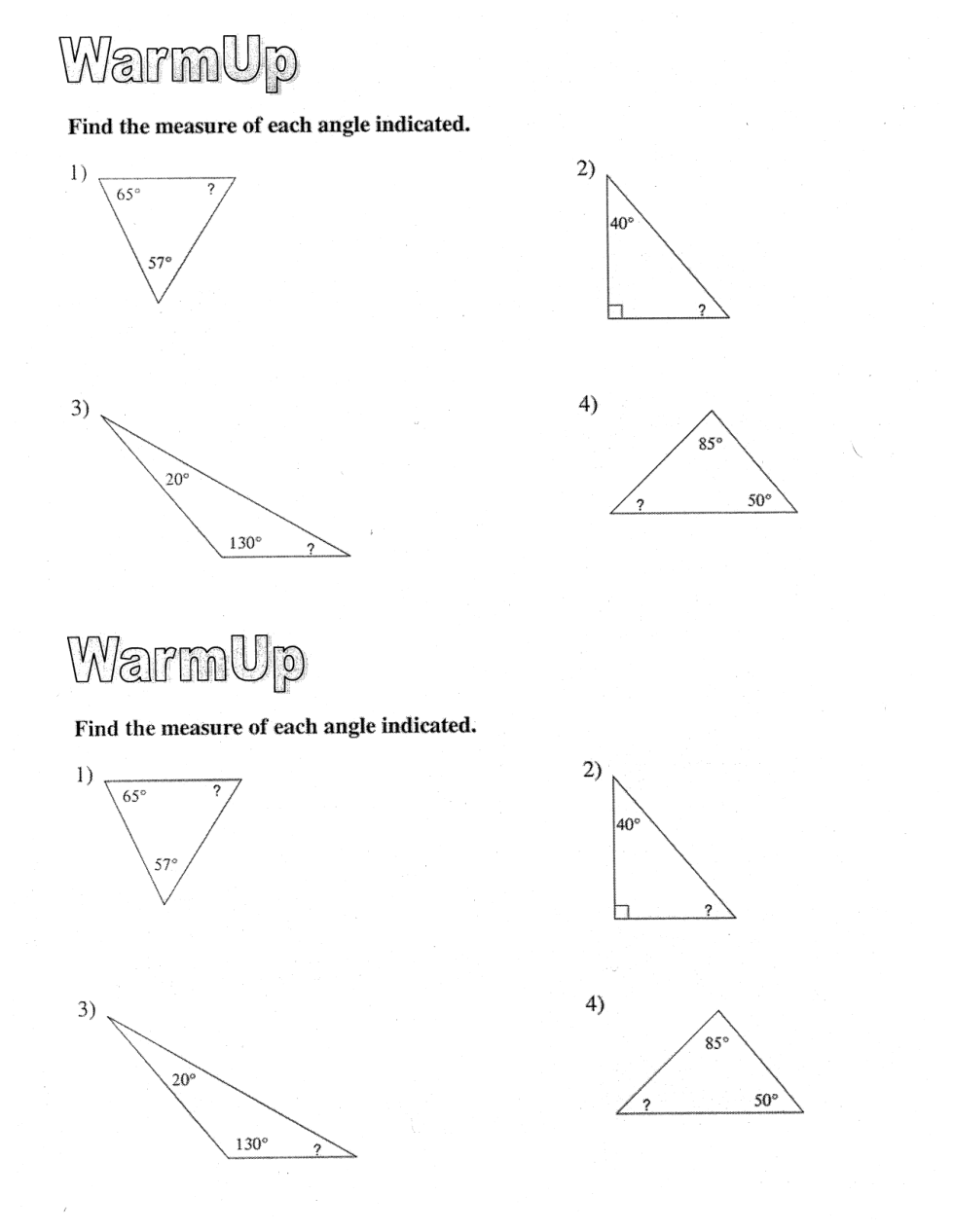
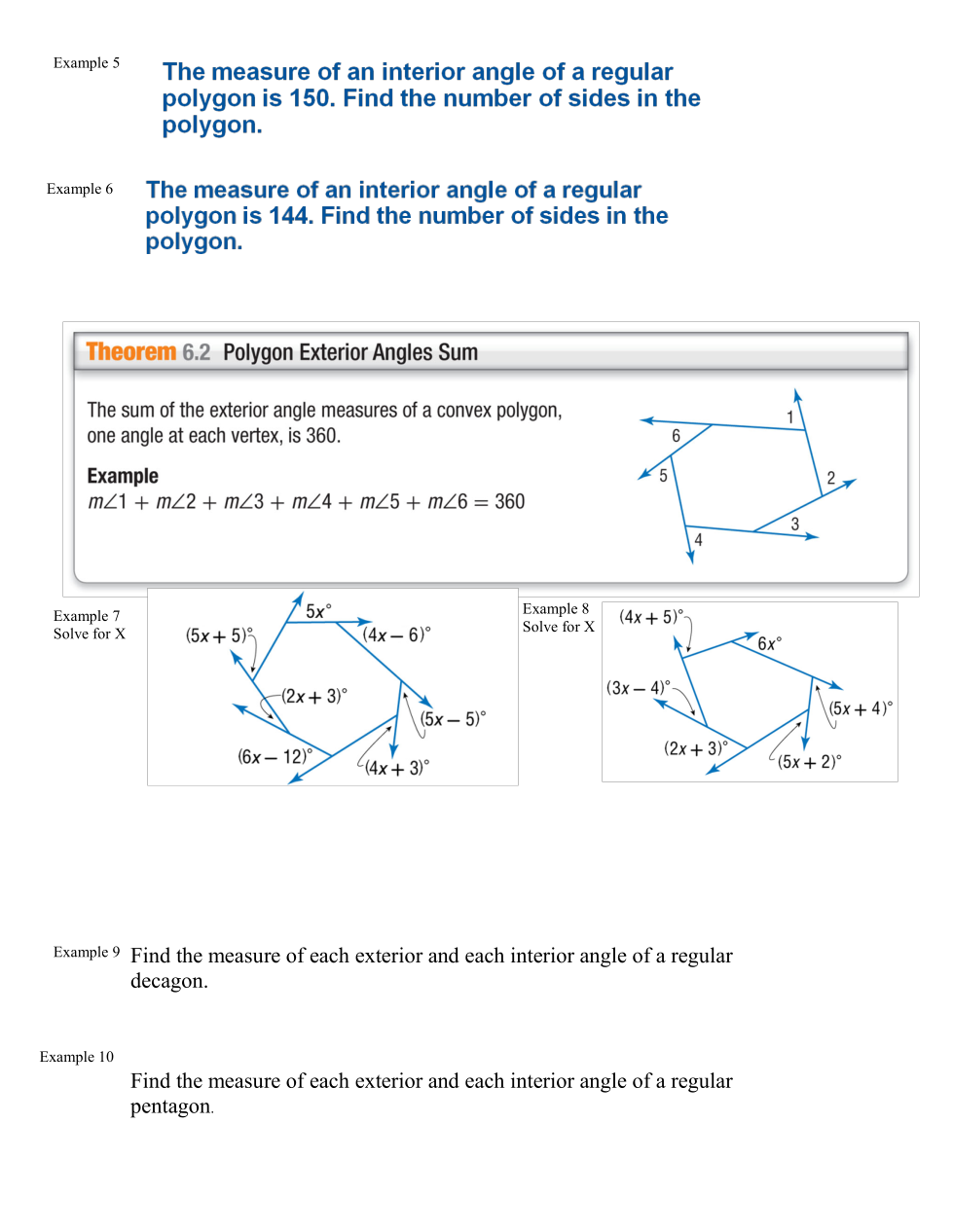
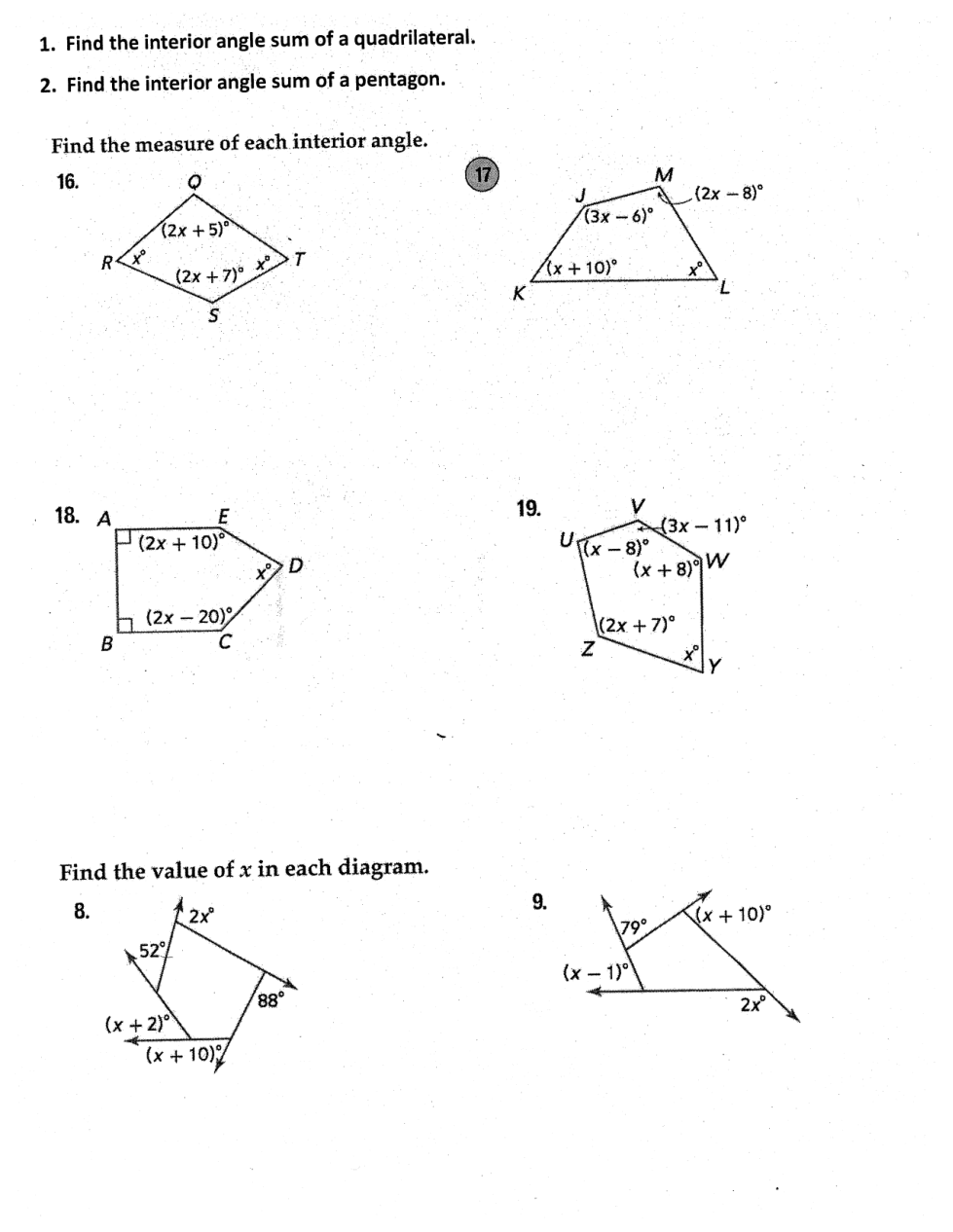
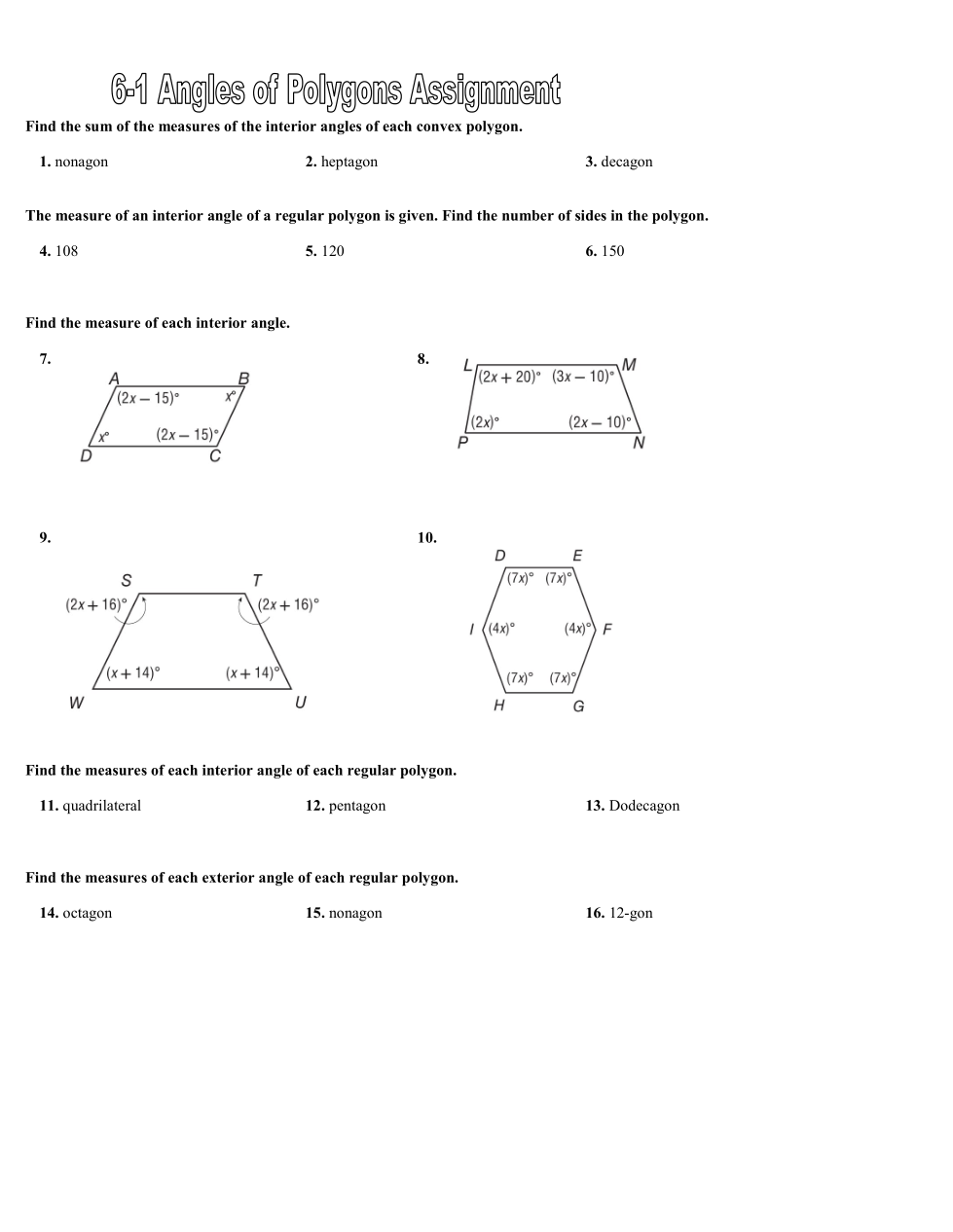
A regular polygon is a polygon where all the sides are the same length and the angles are the same measurement.

n represents the number of sides in the polygon
Like a triangle has three sides. So for a triangle n = 3
A quadrilateral has four sides. So for a quadrilateral n = 4

Interior angle sum formula


Single regular polygon interior angle formula


Exterior angle sum (exterior angles always add up to the same number, 360°)

Single regular polygon exterior angle formula

5.88

quadrilateral has 4 sides. So plugging into the formula.

(4-2) • 180

5.88

5.88

Find the value of x.


This is a quadrilateral. 4 sides.
So first
(4-2)•180
equals 360°.
So the 4 angles add up to 360.

x+(2x+5)+x+(2x+7) = 360

Then solve for x.

5.88


This is a quadrilateral. The 4 angles add up to 360.

Solve for x.

5.88


From the value of x that you had from the previous problem now find the measurement of angle K.

5.88

This is a pentagon.

(5-2)•180

540°

So in a pentagon the 5 angles add up to 540°

90°+(2x+10)°+x°+(2x-20)°+90°=540°

Solve for x.

5.88

This is a pentagon. The 5 angles add up to 540°

Find the value of x.

5.88

From the value of x that you had from the previous problem now find the measurement of angle Z.

5.88

These are exterior angles. Remember that the exterior angles always add up to 360°.

So

2x+88+x+10+x+2+52=360

Solve for x.

5.88

Solve for x.

5.88

Find the sum of the measures of the angles of a nonagon. (9 sides)

(n-2) • 180

(9-2) • 180

5.88

Find the sum of the measures of the angles of a heptagon. (7 sides)

(n-2) • 180

5.88

Find the measure of each interior angle of a regular quadrilateral.
n = 4

Here is the formula for this
So plugging in 4 for n.

5.88

Find the measure of each interior angle of a regular pentagon.
n = 5

Here is the formula for this

5.88

Find the measure of each angle of a regular octagon.
n = 8

So plugging in 8 for n

5.88

Find the measure of each angle of a regular nonagon.
n = 9