Sign up for FREE

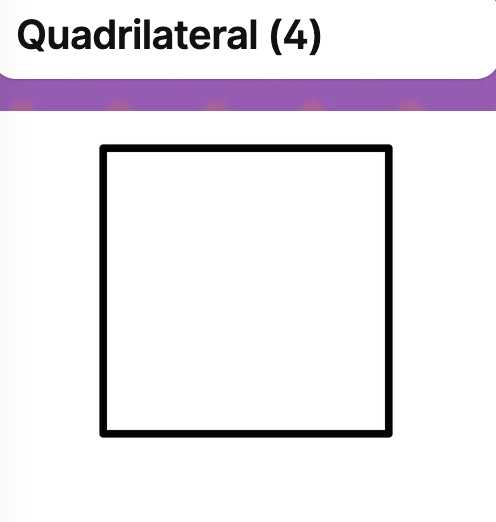
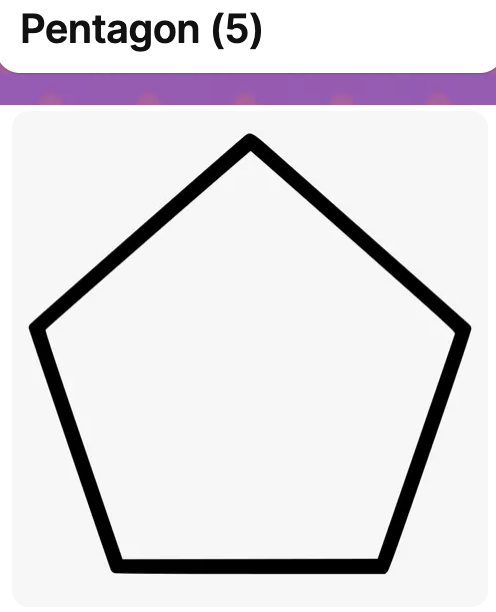
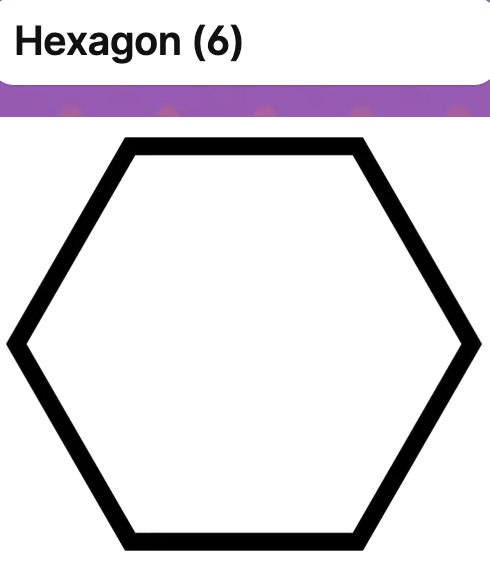
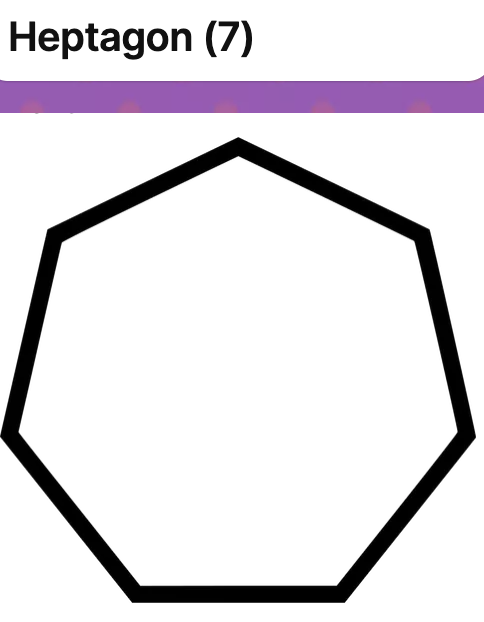
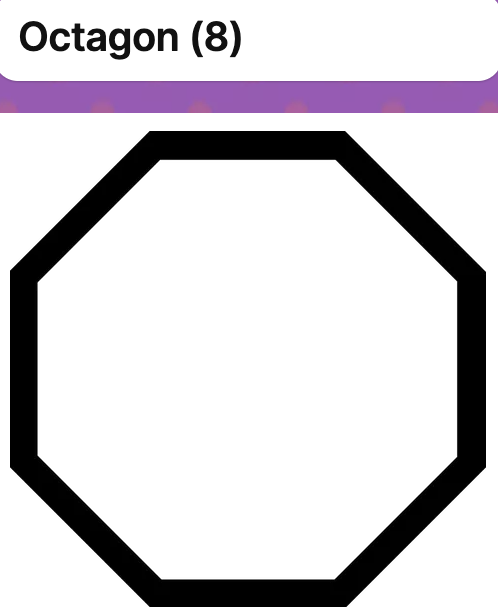
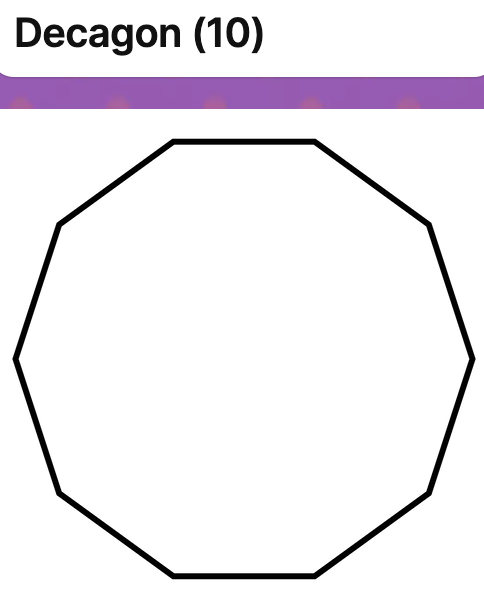
Investigation: Total Interior Angle in a Polygon

Last updated almost 3 years ago

16 questions

1

1

In this exercise, you will figure out a general rule to describe the sum of internal angles in a triangle. 

Step 1:
Split each diagram into triangles in such a way that you are only splitting the angles at each vertex. 

Step 2: 
Use your understanding of the sum of the interior angles of a triangle to find the total interior angle of the shape in question.

Step 3:
Compare all the values of every shape and figure out a general rule for a polynomial of any number of sides. 

1

Question 1

1.

Use a single line to break the quadrilateral into 2 triangles.

1

Question 2

2.

Hence calculate the sum of the total interior angles of a quadrilateral.

1

Question 3

3.

Use two lines to break the pentagon into 3 triangles.

1

Question 4

4.

Hence calculate the sum of the total interior angles of a pentagon.

1

Question 5

5.

Use three lines to break the hexagon into 4 triangles.

1

Question 6

6.

Hence calculate the sum of the total interior angles of a hexagon.

1

Question 7

7.

Use four lines to break the heptagon into 5 triangles.

1

Question 8

8.

Hence calculate the sum of the total interior angles of a heptagon.

1

Question 9

9.

Use five lines to break the octagon into 6 triangles.

1

Question 10

10.

Hence calculate the sum of the total interior angles of an octagon.

1

Question 11

11.

Use six lines to break the nonagon into 7 triangles.

1

Question 12

12.

Hence calculate the sum of the total interior angles of a nonagon.

1

Question 13

13.

Use seven lines to break the decagon into 8 triangles.

1

Question 14

14.

Hence calculate the sum of the total interior angles of a decagon.

Question 15

15.

Complete the table below using the information you gathered so far.

Question 16

16.

What connection can you see between the number of triangles, the number of sides of a polygon and the total interior angle? Can you write the relationship as an equation?