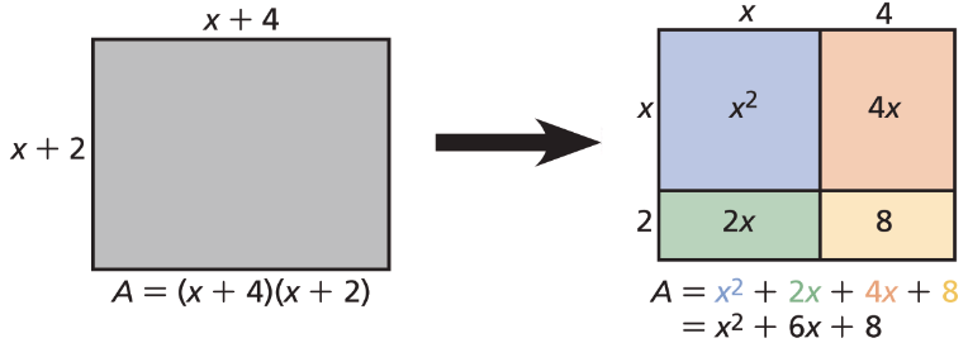
Lesson 4.3 Multiplying Polynomials
star
star
star
star
star
Last updated over 1 year ago
11 questions
Note from the author:
Learning Goal: I can add, subtract, and multiply polynomial expressions, including those representing real-world situations.
Learning Goal: I can add, subtract, and multiply polynomial expressions, including those representing real-world situations.
Guided Notes
1
1
1
1
1
On Your Own
4
2
3
3
4
4