Points, Lines, and Planes Practice

5

Match each term with its correct definition.

Draggable item		Corresponding Item
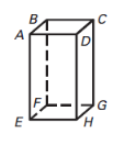
Line		A location in space which has no dimension (no length, no area, no volume).
Line Segment		An infinite set of points which has one dimension. Extends in opposite directions.
Point		An infinite set of points with two dimensions. Extends in all directions.
Ray		Infinite set of points consisting of two endpoints and all the points in between.
Plane		Infinite set of points consisting of one endpoint (the initial point) and all the points extending in one direction.

7

Match each term with its correct definition.

Draggable item		Corresponding Item
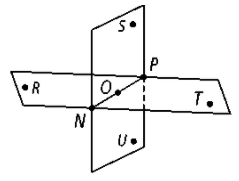
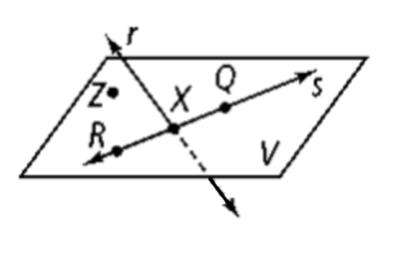
Noncollinear		Two points are always _____ because a line can always be placed through them.
Parallel Lines		Three or more points which are situated such that a line cannot be placed through all of them.
Coplanar		Points and/or lines that are located on the same plane are said to be _____ .
Noncoplanar		Points and/or lines that are NOT located on the same plane are said to be.
Parallel Planes		Lines that are coplanar and do not intersect.
Skew Lines		Two planes that do not intersect.
Collinear		Lines that are noncoplanar and do not intersect.

1

What is/are correct ways to refer to this geometric figure?

1

What is/are correct ways to refer to this geometric figure?

1

What is/are correct ways to refer to this geometric figure?

1

In the diagram shown here, line m and line n are

1

In the diagram shown here, line m and line n are

1

The planes shown below are

1

Which of the following is a TRUE statement regarding the diagram shown here?

1

Given the diagram shown below, which of the following are a TRUE statements? Select all that apply.

1

How many segments can be named from the figure shown here? Just type the number.

1

Any two points are collinear.

1

Any three points are collinear.

1

Any three points are coplanar.

1

Any four points are coplanar.

1

Two lines can intersect at more than one point.

1

Two lines always intersect at exactly one point.

1

If two lines intersect, then they can only intersect at exactly one point.

1

Any two planes will intersect one another.

1

If two planes intersect, they intersect at exactly one point.

1

If two planes intersect, a segment is formed at their intersection.

1

If two planes intersect, a line is formed at their intersection.

1

Describe the intersection of plane Q and plane P shown here.

1

Which of the following ARE appropriate ways to refer to the plane shown below? Select all that apply.

1

Is it appropriate to refer to Plane W in the diagram below as Plane ATB ? Hint: notice that Plane Z also passes through those same three points.

Use the diagram shown to answer the following questions.

1

Points S and T are collinear.

1

Use the diagram shown to answer the following questions.

1

Use the diagram shown to answer the following questions.

1

Line r and line s are coplanar lines because they are both located on Plane V.

1

Points, Lines, and Planes Practice

Match each term with its correct definition.

Match each term with its correct definition.

What is/are correct ways to refer to this geometric figure?

What is/are correct ways to refer to this geometric figure?

What is/are correct ways to refer to this geometric figure?

In the diagram shown here, line m and line n are

In the diagram shown here, line m and line n are

The planes shown below are

Which of the following is a TRUE statement regarding the diagram shown here?

Given the diagram shown below, which of the following are a TRUE statements? Select all that apply.

How many segments can be named from the figure shown here? Just type the number.

Any two points are collinear.

Any three points are collinear.

Any three points are coplanar.

Any four points are coplanar.

Two lines can intersect at more than one point.

Two lines always intersect at exactly one point.

If two lines intersect, then they can only intersect at exactly one point.

Any two planes will intersect one another.

If two planes intersect, they intersect at exactly one point.

If two planes intersect, a segment is formed at their intersection.

If two planes intersect, a line is formed at their intersection.

Describe the intersection of plane Q and plane P shown here.

Which of the following ARE appropriate ways to refer to the plane shown below? Select all that apply.

Is it appropriate to refer to Plane W in the diagram below as Plane ATB ? Hint: notice that Plane Z also passes through those same three points.

Points S and T are collinear.

Line r and line s are coplanar lines because they are both located on Plane V.

Match each term with its correct definition.

Match each term with its correct definition.

What is/are correct ways to refer to this geometric figure?

What is/are correct ways to refer to this geometric figure?

What is/are correct ways to refer to this geometric figure?

In the diagram shown here, line m and line n are

In the diagram shown here, line m and line n are

The planes shown below are

Which of the following is a TRUE statement regarding the diagram shown here?

Given the diagram shown below, which of the following are a TRUE statements? Select all that apply.

How many segments can be named from the figure shown here? Just type the number.

Any two points are collinear.

Any three points are collinear.

Any three points are coplanar.

Any four points are coplanar.

Two lines can intersect at more than one point.

Two lines always intersect at exactly one point.

If two lines intersect, then they can only intersect at exactly one point.

Any two planes will intersect one another.

If two planes intersect, they intersect at exactly one point.

If two planes intersect, a segment is formed at their intersection.

If two planes intersect, a line is formed at their intersection.

Describe the intersection of plane Q and plane P shown here.

Which of the following ARE appropriate ways to refer to the plane shown below? Select all that apply.

Is it appropriate to refer to Plane W in the diagram below as Plane ATB ? Hint: notice that Plane Z also passes through those same three points.

Points S and T are collinear.

Points R, S, and T are coplanar.

Which of the following points are NOT coplanar with points R, O, and T? Select all that apply.

Which point is coplanar with points A, B, and E?

Which point is coplanar with points A, B, and G?

What is the intersection of planes EFG and CDG?

Which plane is parallel to plane ADE?

Line r and line s are coplanar lines because they are both located on Plane V.

Line r and line s are coplanar lines because a plane could be passed through both of them.

Part of line r is dotted because

When naming the plane by points, any three of the letters R, Q, X, and Z can be used, but not letters s or V. What are the two reasons for this?

Points R, S, and T are coplanar.

Which of the following points are NOT coplanar with points R, O, and T? Select all that apply.

Which point is coplanar with points A, B, and E?

Which point is coplanar with points A, B, and G?

What is the intersection of planes EFG and CDG?

Which plane is parallel to plane ADE?

Line r and line s are coplanar lines because a plane could be passed through both of them.

Part of line r is dotted because

When naming the plane by points, any three of the letters R, Q, X, and Z can be used, but not letters s or V. What are the two reasons for this?