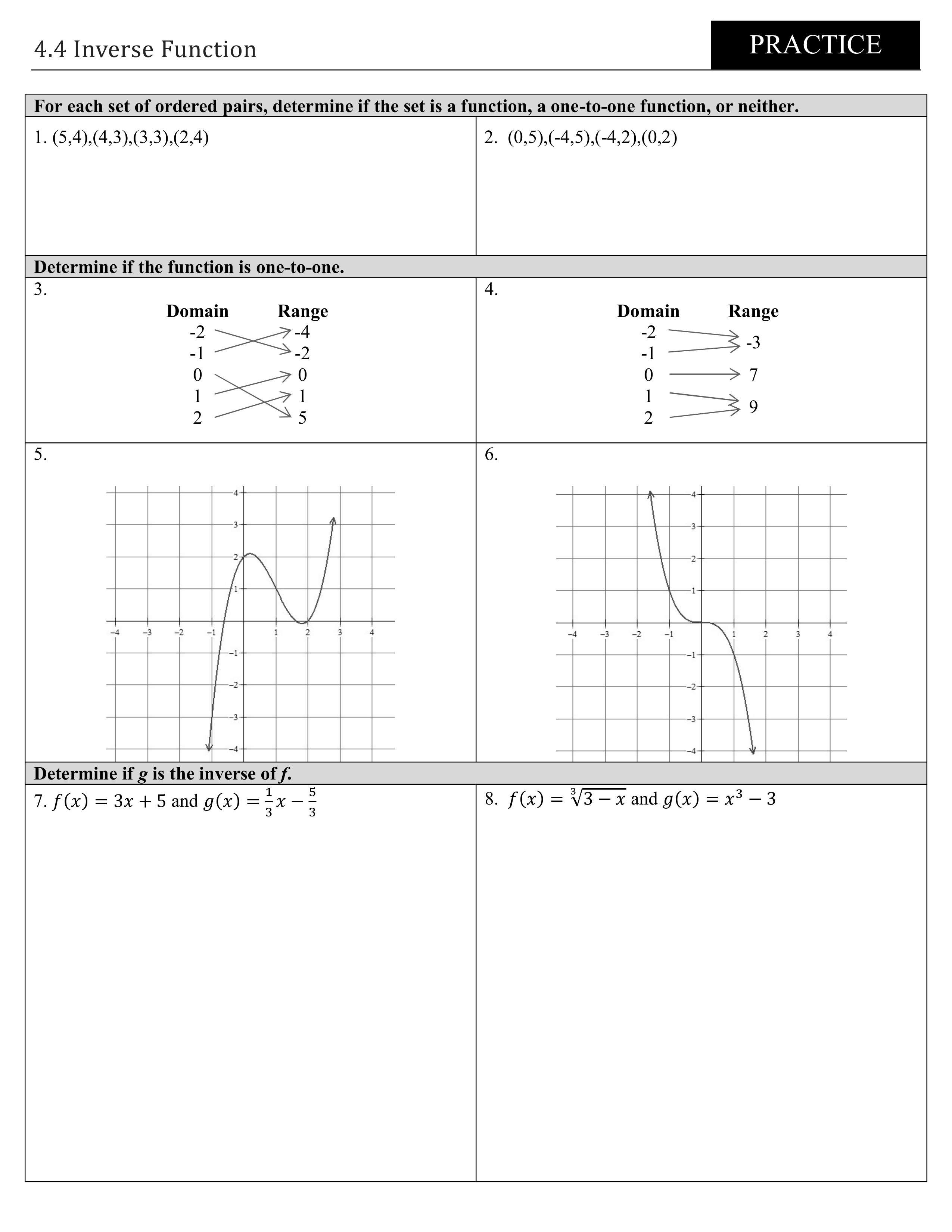
S2w1 FC Graphing and inverting trig functions
star
star
star
star
star
Last updated 5 months ago
31 questions
1
1
Required
1
Required
1
1
Required
1
1
Required
1
Required
1
Required
1
Required
1
1
1
1
1
1
1
1
1
1
1
1
Required
1
| Draggable item | arrow_right_alt | Corresponding Item |
|---|---|---|
45 | arrow_right_alt | 0 |
60 | arrow_right_alt | |
210 | arrow_right_alt | |
360 | arrow_right_alt | |
270 | arrow_right_alt | |
300 | arrow_right_alt | |
135 | arrow_right_alt | |
0 | arrow_right_alt | |
315 | arrow_right_alt | |
120 | arrow_right_alt | |
30 | arrow_right_alt |