S2W3 FC#2 - identities practice
star
star
star
star
star
Last updated 5 months ago
10 questions
1
1
1
1
1
10
0
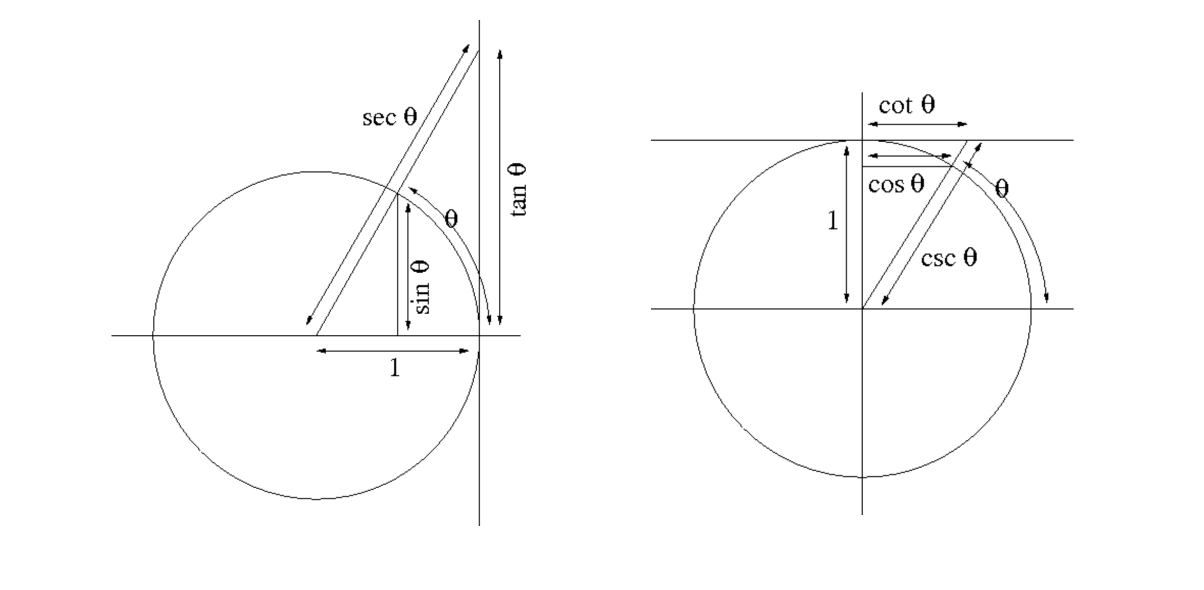
| Draggable item | arrow_right_alt | Corresponding Item |
|---|---|---|
sec x | arrow_right_alt | cos (90°-x) |
tan x | arrow_right_alt | cot(90°-x) |
cot x | arrow_right_alt | csc (90°-x) |
cos(x) | arrow_right_alt | 1/sin x |
| arrow_right_alt | cos x/sin x | |
csc x | arrow_right_alt | 1 |
| arrow_right_alt | ||
sin x | arrow_right_alt | |
| arrow_right_alt | cos(-x) |