Log inSign up for FREE
Library

s2w4 Precalc FC Laws of sine and cosine

Last updated 3 months ago
29 questions
1
1
1

one of the reasons to use identities is so you can rewrite an equation so that there is only one trig function involved. rewrite this equation so that is is only one trig function

1

Is the following an identity?

1

Lets review congruent vs similar triangles - what is the difference?

1

Lets review congruent triangles: you know two triangles are congruent if

1

The angles of a triangle add up to

1

These two triangles are congruent by

1

These two triangles are congruent by

1

These two triangles are congruent by

1

These two triangles are congruent by

1

These two triangles are congruent by

1

These two triangles are congruent by

1
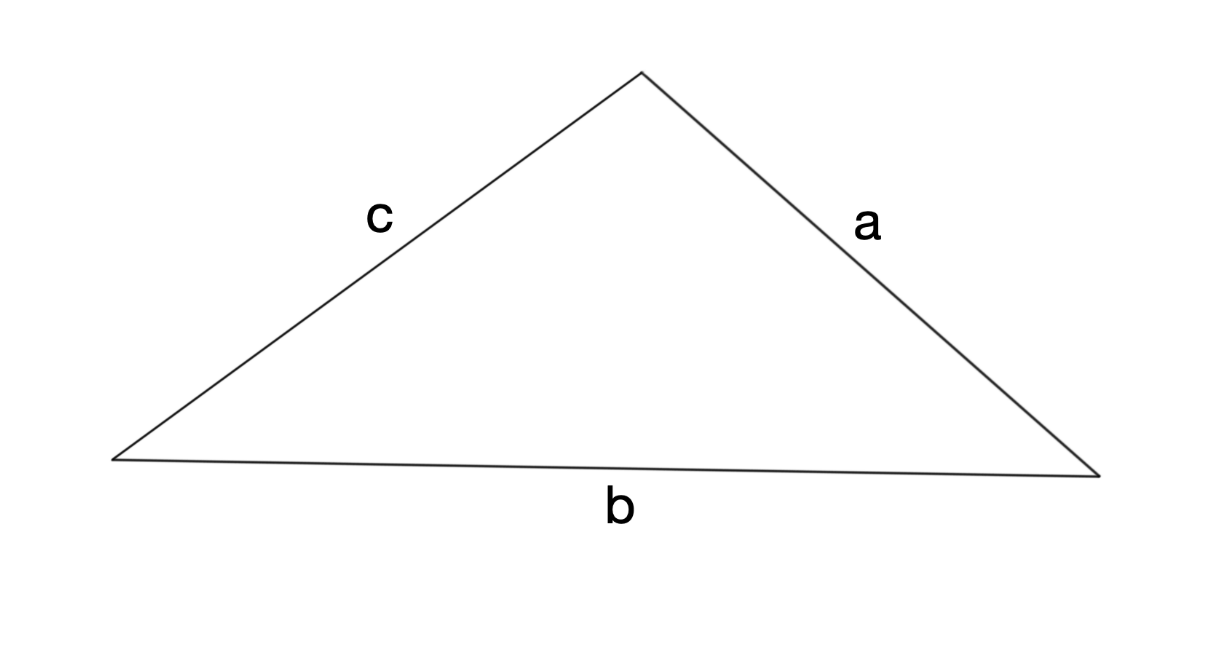
ok, up until know, trig has been all about the right triangles. But we are about to push a little beyond that. This is called the law of sines


for ANY triangle, where A is the side opposite angle a, B is the side opposite angle b, and C is the side opposite angle C. Given this triangle with sides a, b and c, drag A B and C to their proper angles.
Other Answer Choices:
C
B
A
1

Lets go over why SSA is the "ambiguous case" You will see at the top of this image a line. there is a line segment connected to this line at 31.9°, and the line segment is length 0. So far we do not have a triangle, but we do have

1

I know the second side i want is 4, so to construct my 31.9°, 6,4 triangle, I draw a circle of radius four around my point B. How many times does that circle touch my line?

1

Name the two triangles in my diagram that have a 31.9° angle, and two sides, 4 and 6 units long

1

setting up Law of Sine's here, I get
AND

What do you think the relationship is between angle BCD and angle BDA is?

1

At what angle would the radius of circle B only touch that initial line once?

1

There is also a law of cosines. it is SIGNIFICANTLY uglier

where c is the angle opposite B.
you might want to pause now and go practice law of sines in aleks homework and the modules.

1

Given the following information about a triangle, which law can you use to find all the other sides?

  • Side, angle, side
  • Angle, side, angle
  • angle, angle, side
  • side, side, angle
  • side, side, side
  • angle, angle, angle
  • Law of sines
  • Law of cosines
  • this does not describe just one triangle
1

this looks a little like the odd and even function thing - whats the connection?

1

you'll notice this is the same relationship as the SSA triangle that the sin law didn't help with a couple questions ago. Is there a relationship between cos a and cos (180-a)?

1

I don't remember the intersecting chord theorem. Do you?

3
Solve the triangle using Law of Sines.

a=_______ , b=_______ , C=_______ °
you will want to solve for angle C first, and round the lengths to the hundreth place. note that C should be in degrees.
1
solve the triangle using law of cosines
a = 6, b=10, c=11
A=_______ °, B=_______ °, C=_______ °
round to the nearest hundreth,
1

draw the triangle described above. to find the area of the triangle, you need to find the height, how can you do that?

1

watching the proofs helps me understand the laws

1

categorize

  • what the law of sines is
  • what the law of cosines is
  • when to use the law of sines
  • when to use the law of cosines
  • how to simplify or rearrange trig expressions using the identities I know
  • when are triangles congruent
  • why SSA gives an ambiguous case
  • how to use the law of sin to find the area of triangle
  • ive got this
  • im fuzzy
  • so confused