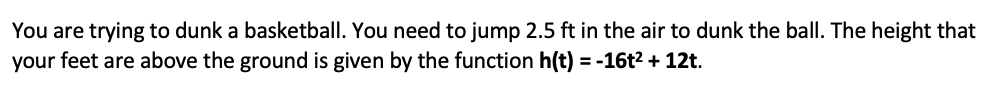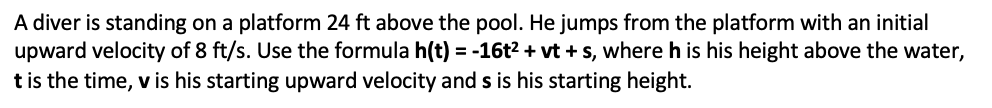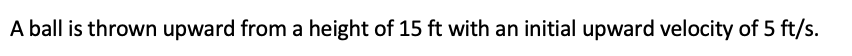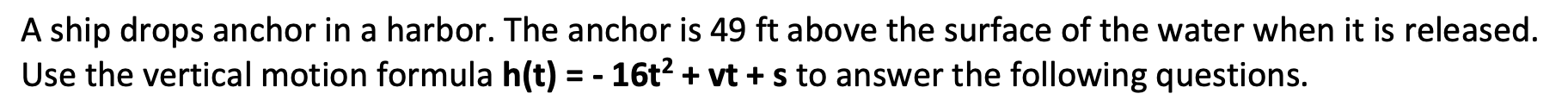How long did it take Jason, in seconds, to reach his maximum height?
What was the highest point, in feet, that Jason reached?
Jason hit the water after how many seconds?
How long, in seconds, will it take for the rocket to return to the ground?
How long, in seconds, will it take the rocket to reach its maximum height?
What is the maximum height, in feet, reached by the rocket?
How long, in seconds, will the rocket take to hit the ground after it is launched?
Round to the nearest tenth of a second.
What is the maximum height, in feet, of the grappling hook?
Can you throw it high enough to reach the ledge?
What is the maximum height, in feet, your feet will be above the ground?
Will you be able to dunk the basketball?
How long, in seconds, will it take the diver to hit the water?
Use the formula
If the bell is 25 ft above the ground, will it be hit by the ball?
Support your answer to #16.
What is the value of s, the starting height?
What is the value of h when the anchor hits the water?
The starting velocity is zero. After how many seconds will the anchor hit the water?
An amateur rocketry club is holding a competition. There is cloud cover at 1000 ft.If a rocket is launched with a velocity of 315 ft/s, use the function h(t) = -16t2 + vt + h0 to determine how long the rocket is out of sight.
A trebuchet launches a projectile on a parabolic arc from a height of 47 ft at a velocity of 40 ft/s.
Using the function h(t) = -16t2 + vt + h0 , determine when the projectile will first reach a height of 60 ft.
How many seconds will take the projectile to, again, reach 60 feet?
During World War I, mortars were fired from trenches 3 feet down. The mortars had a velocity of 150 ft/s.
Determine how long it will take for the mortar shell to strike its target.
How high is the target?
After how many seconds will the rocket be 112 feet above the ground?
