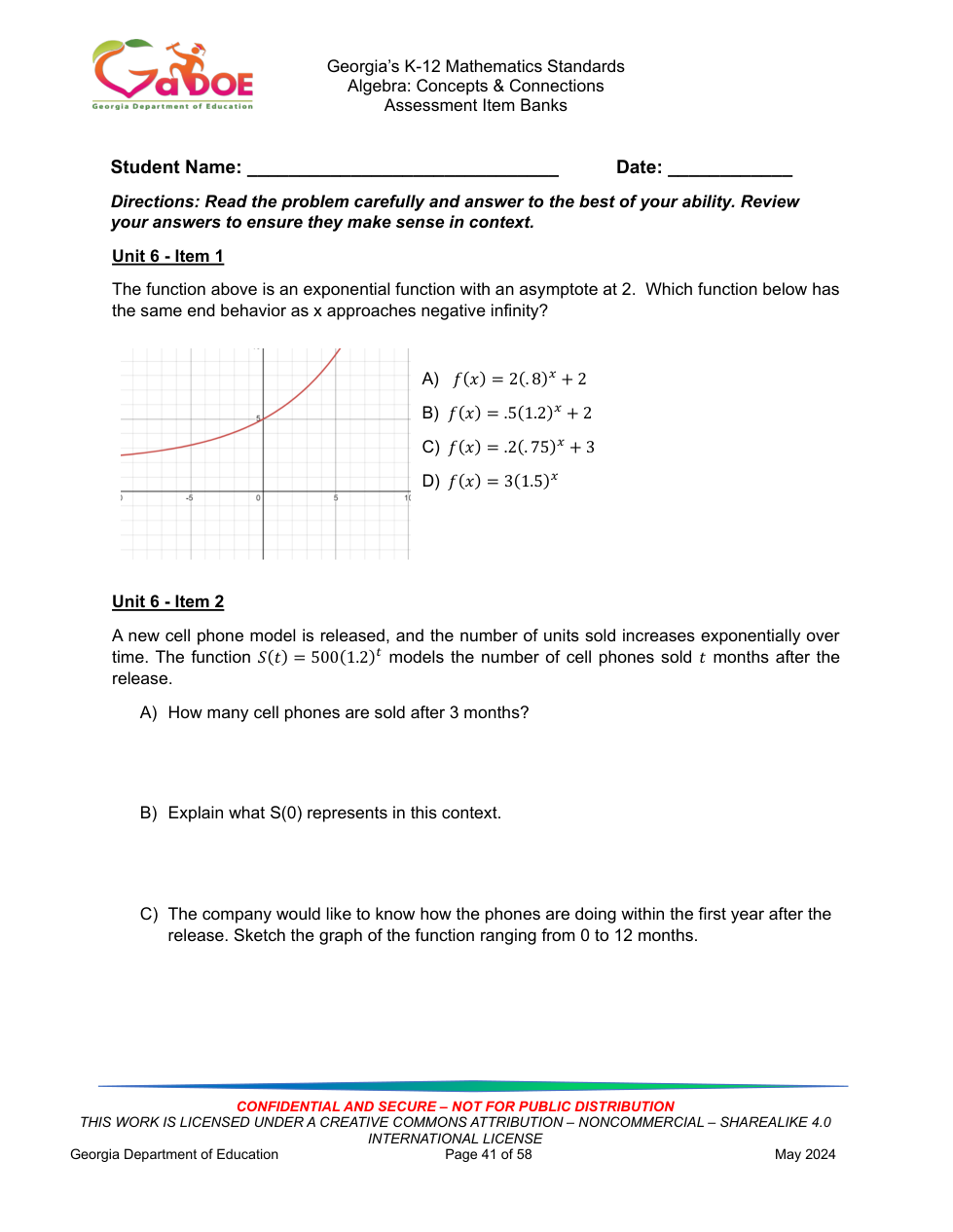
Algebra: Unit 6
star
star
star
star
star
Last updated 12 months ago
16 questions
1
Unit 6 - Item 6Given the following function of 𝑓(𝑥) = −32 + 𝑘, what will happen to the graph if you substitutenegatives versus positives for “𝑘”? Explain.
Unit 6 - Item 6
Given the following function of 𝑓(𝑥) = −32 + 𝑘, what will happen to the graph if you substitute
negatives versus positives for “𝑘”? Explain.
A.FGR.9.1