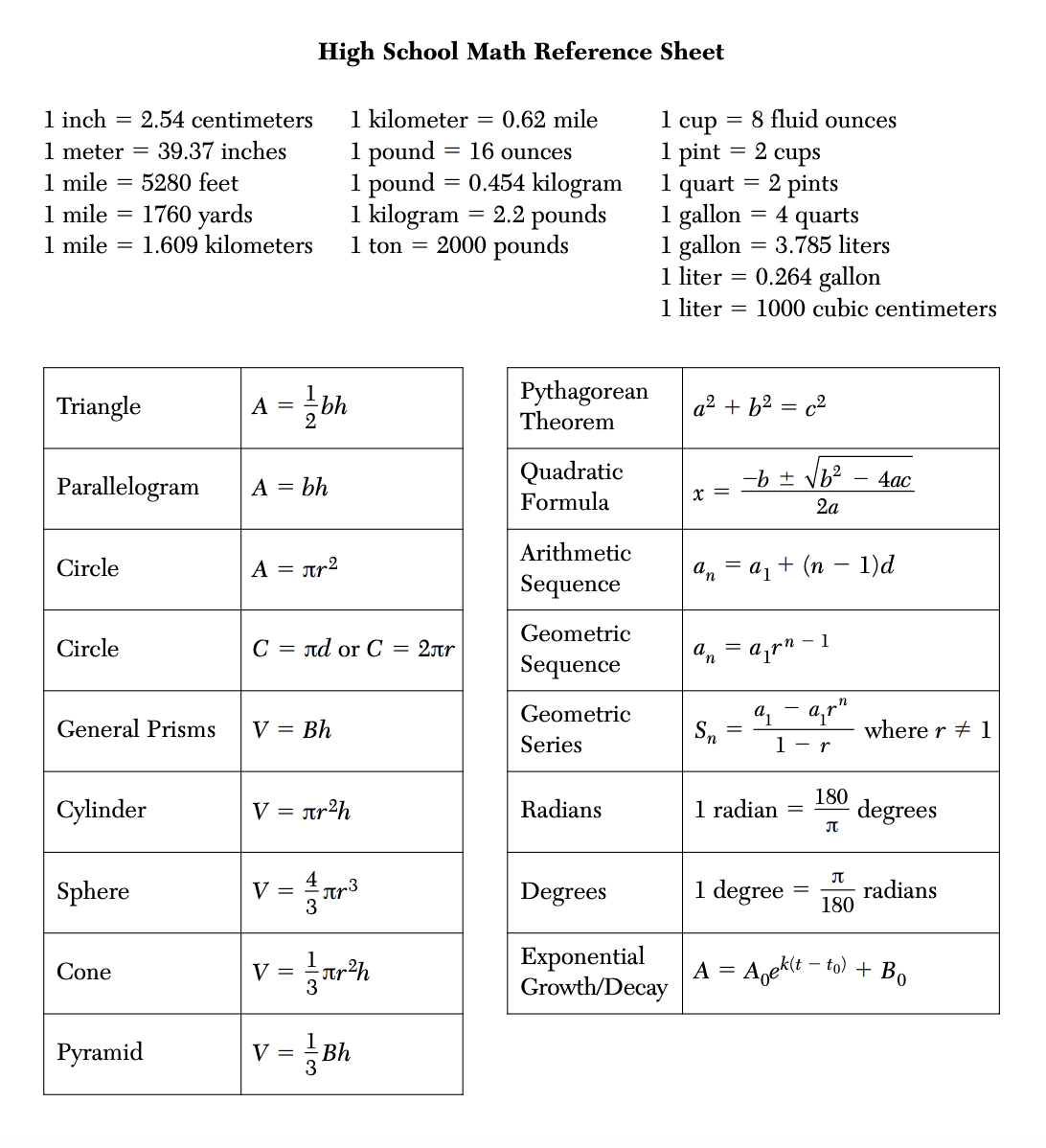
NYSED High School Regents Algebra I
star
star
star
star
star
Last updated 10 months ago
37 questions
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
2
Required
4
Required
4
Required
4
Required
4
Required
6