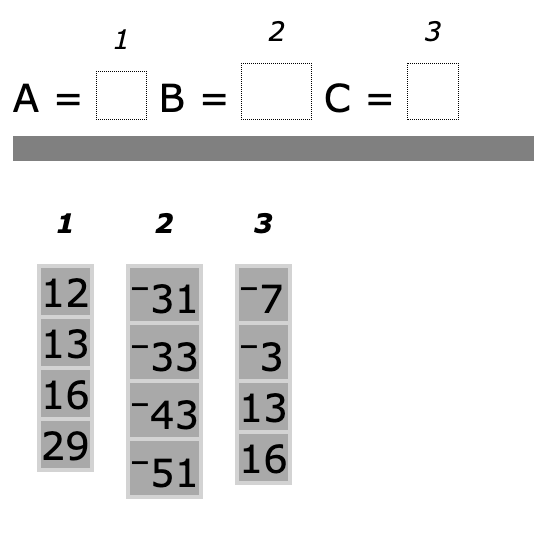
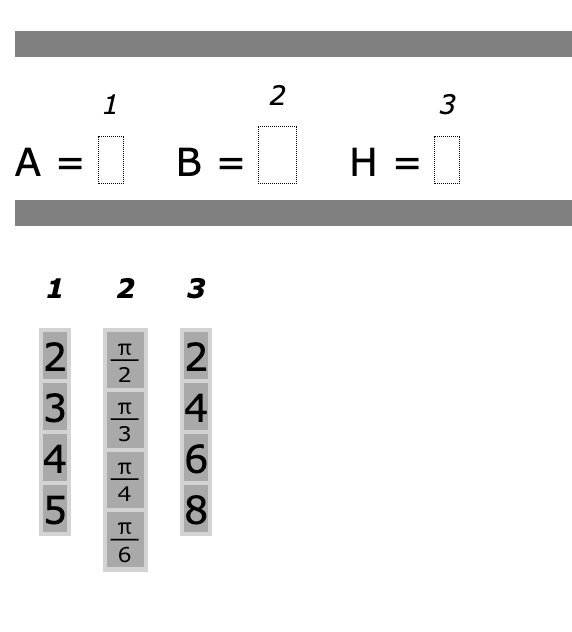
End-of-Course (EOC) Math 3
star
star
star
star
star
Last updated 8 months ago
30 questions
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1
Required
1