Log inSign up for FREE
Library

1.2 Data, Sampling, and Variation in Data and Sampling (4/21/2025)

Last updated 8 months ago
14 questions
Untitled Section 1
1
Given the definitions of Qualitative and Quantitative make an educated guess where these would be placed

Qualitative data are the result of categorizing or describing attributes of a population.

Quantitative data are the result of counting or measuring attributes of a population.

Hair Color __________

Money __________

Blood Type __________

Number or students in school __________

Jersey Number__________
Examples
Discrete vs Continuous

Quantitative Discrete data that can only take certain numerical values

example, number of phone calls a day, money a person has, steps you take a day

Quantitative Continuous Data data that is not made up of counting numbers, but that may include fractions, decimals, or irrational numbers.

examples, length, weights, times
1
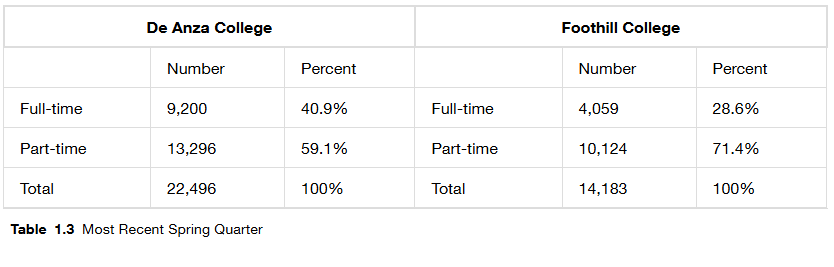
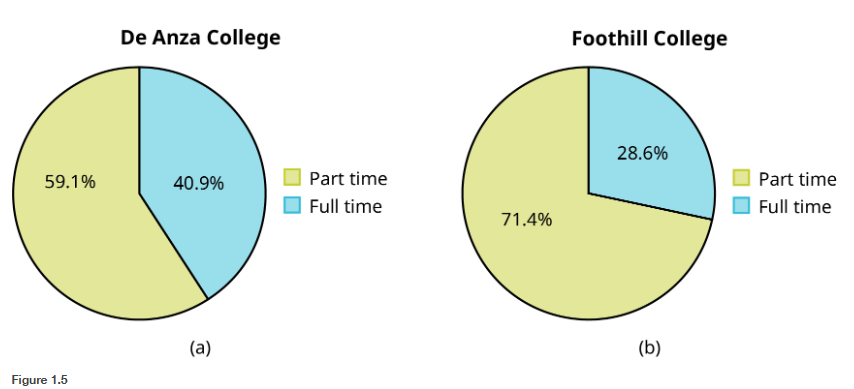
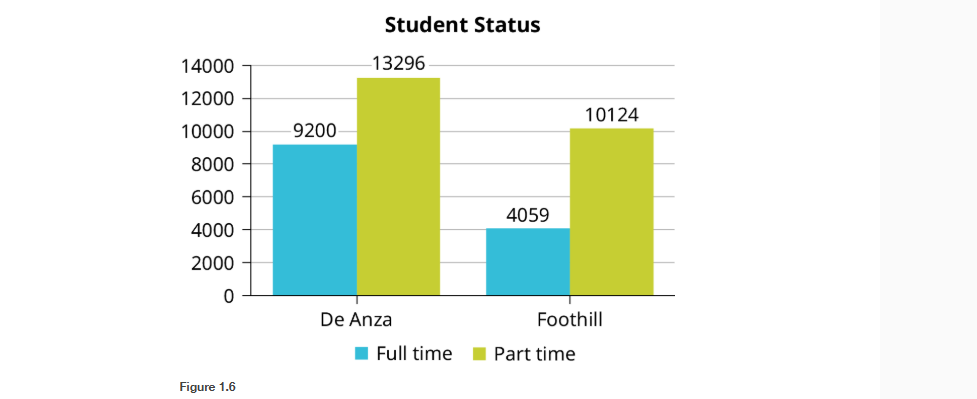
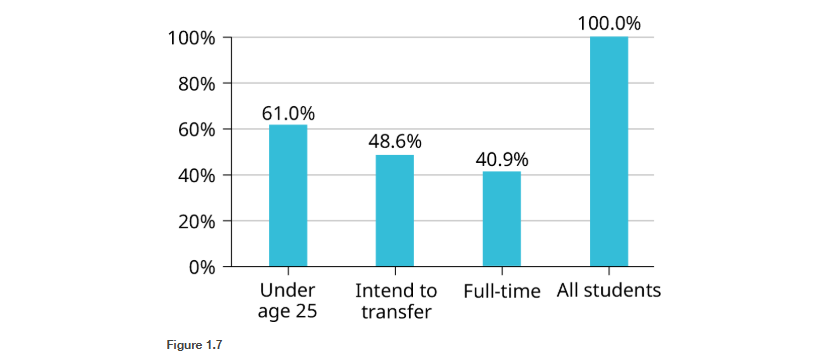
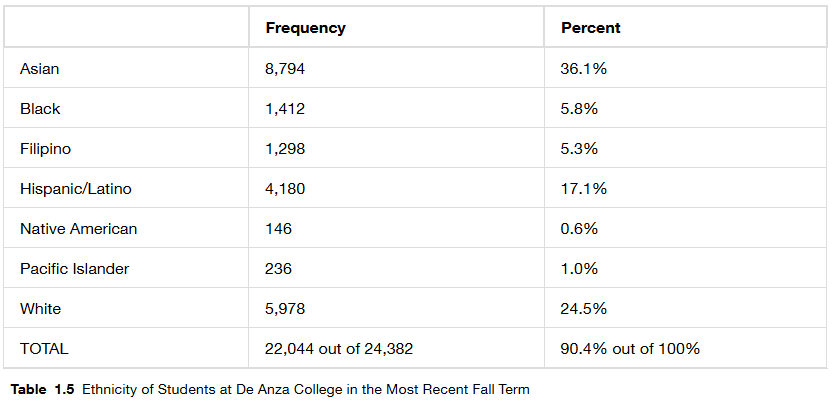
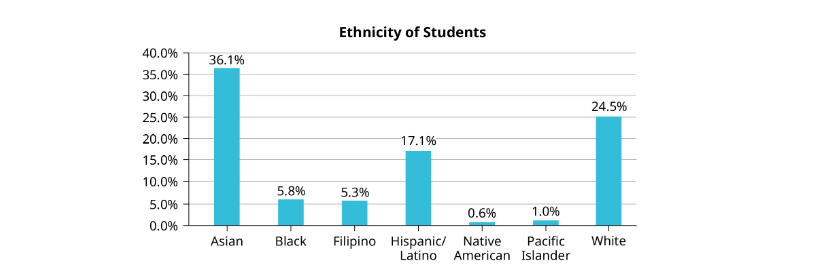
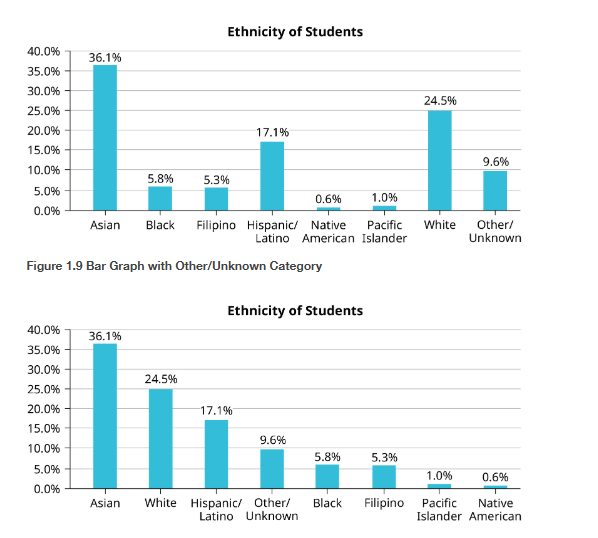
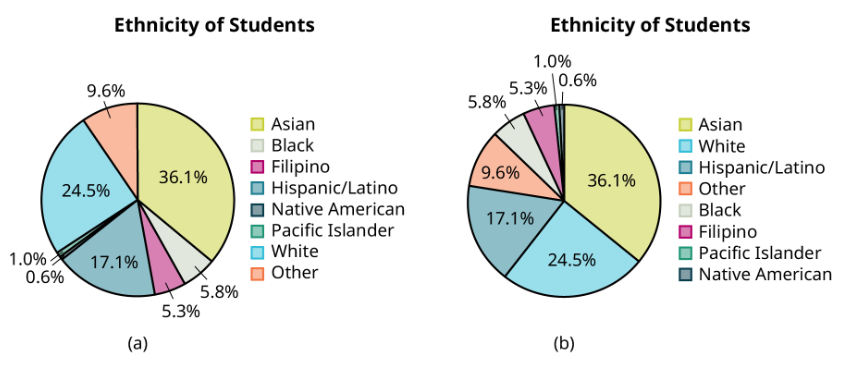
Based on those previous definitions, determine which of these are qualitative, quantitative continuous or discrete data

The data are the number of books students carry in their backpacks. You sample five students. Two students carry three books, one student carries four books, one student carries two books, and one student carries one book.
__________

The data are the weights of backpacks with books in them. You sample the same five students. The weights (in pounds) of their backpacks are 6.2, 7, 6.8, 9.1, 4.3. Notice that backpacks carrying three books can have different weights.
__________

The data are the colors of backpacks. Again, you sample the same five students. One student has a red backpack, two students have black backpacks, one student has a green backpack, and one student has a gray backpack.
__________

The data are the areas of lawns in square feet. You sample five houses. The areas of the lawns are 144 sq. feet, 160 sq. feet, 190 sq. feet, 180 sq. feet, and 210 sq. feet. What type of data is this?
__________

The data are the colors of houses. You sample five houses. The colors of the houses are white, yellow, white, red, and white.
__________

The data are the number of machines in a gym. You sample five gyms. One gym has 12 machines, one gym has 15 machines, one gym has ten machines, one gym has 22 machines, and the other gym has 20 machines.
__________
Untitled Section 4
1
Based on the prompt below, give an example of a qualitative data, quantitative discrete data, and quantitative continuous data.

You go to the supermarket and purchase three cans of soup (19 ounces tomato bisque, 14.1 ounces lentil, and 19 ounces Italian wedding), two packages of nuts (walnuts and peanuts), four different kinds of vegetable (broccoli, cauliflower, spinach, and carrots), and two desserts (16 ounces pistachio ice cream and 32 ounces chocolate chip cookies).


qualitative data: _______

quantitative discrete data: _______

quantitative continuous data: _______
1
Based on those previous definitions, determine which of these are qualitative, quantitative continuous or discrete data

a. The number of pairs of shoes you own__________

b. The type of car you drive __________

c. The distance it is from your home to the nearest grocery store__________

d. The number of classes you take per school year __________

e. The type of calculator you use __________

f. Weights of dogs at an animal shelter __________

g. Number of correct answers on a quiz __________

h .A statistics professor collects information about the classification of her students as first-year students, sophomores, juniors, or seniors.
__________

i. The registrar at State University keeps records of the number of credit hours students complete each semester. The data collected are summarized in the histogram. The class boundaries are 10 to less than 13, 13 to less than 16, 16 to less than 19, 19 to less than 22, and 22 to less than 25.

__________
Qualitative Data Discussion
Below are tables comparing the number of part-time and full-time students at De Anza College and Foothill College enrolled for the most recent spring quarter. The tables display counts (frequencies) and percentages or proportions (relative frequencies). The percent columns make comparing the same categories in the colleges easier. Displaying percentages along with the numbers is often helpful, but it is particularly important when comparing sets of data that do not have the same totals, such as the total enrollments for both colleges in this example. Notice how much larger the percentage for part-time students at Foothill College is compared to De Anza College.

Tables are a good way of organizing and displaying data. But graphs can be even more helpful in understanding the data. There are no strict rules concerning which graphs to use. Two graphs that are used to display qualitative data are pie charts and bar graphs.
In a pie chart, categories of data are represented by wedges in a circle and are proportional in size to the percent of individuals in each category.
In a bar graph, the length of the bar for each category is proportional to the number or percent of individuals in each category. Bars may be vertical or horizontal.
A Pareto chart consists of bars that are sorted into order by category size (largest to smallest).

Percentages That Add to More (or Less) Than 100%

Sometimes percentages add up to be more than 100% (or less than 100%). In the graph, the percentages add to more than 100% because students can be in more than one category. A bar graph is appropriate to compare the relative size of the categories. A pie chart cannot be used. It also could not be used if the percentages added to less than 100%.
Omitting Categories/Missing Data
The table displays Ethnicity of Students but is missing the "Other/Unknown" category. This category contains people who did not feel they fit into any of the ethnicity categories or declined to respond. Notice that the frequencies do not add up to the total number of students. In this situation, create a bar graph and not a pie chart.
Pie Chart: No Missing Data
Sampling
A sample should have the same characteristics as the population it is representing

Must be a Random Sample

Example is Simple Random Sampling- Each group of size n is likely to be chosen as another group of size n. Examples, pulling names out of a hat, or generating random numbers on a computer to select people

Stratified Sample- Divide the population into groups and take a proportionate simple random sample of each. (ie pick three random students from each classroom)

Cluster Sample- Divide the population into clusters, and randomly select some of the clusters. (ie pick 6 random classrooms and get information from all students)

Systematic Sample- Randomly select a starting point and take every nth piece of data from a listing of the population. (Use student ID's and select every ten students for study)
Non Random Sampling example

Convenience sampling involves using results that are readily available. (only interviewing people that are easily accessible)
Sampling with replacement is truly random sampling (there is a chance to be selected more than once). However, most studies do a random sample without replacement for practical reasons.
Sampling Error the process in which the sampling mistakes occur, like not having a large enough sample

Non- Sampling Errors- Things not to do with sampling mistakes like a faulty machine or bad record keeping.

Sampling Bias- When not all members of the population are likely to be chosen. (i.e, you only ask your friends and family about a study to do with Salinas)
  • Problems with samples: A sample must be representative of the population. A sample that is not representative of the population is biased. Biased samples that are not representative of the population give results that are inaccurate and not valid.
  • Self-selected samples: Responses only by people who choose to respond, such as call-in surveys, are often unreliable.
  • Sample size issues: Samples that are too small may be unreliable. Larger samples are better, if possible. In some situations, having small samples is unavoidable and can still be used to draw conclusions. Examples: crash testing cars or medical testing for rare conditions
  • Undue influence:  collecting data or asking questions in a way that influences the response
  • Non-response or refusal of subject to participate:  The collected responses may no longer be representative of the population.  Often, people with strong positive or negative opinions may answer surveys, which can affect the results.
  • Causality: A relationship between two variables does not mean that one causes the other to occur. They may be related (correlated) because of their relationship through a different variable.
  • Self-funded or self-interest studies: A study performed by a person or organization in order to support their claim. Is the study impartial? Read the study carefully to evaluate the work. Do not automatically assume that the study is good, but do not automatically assume the study is bad either. Evaluate it on its merits and the work done.
  • Misleading use of data: improperly displayed graphs, incomplete data, or lack of context
  • Confounding:  When the effects of multiple factors on a response cannot be separated.  Confounding makes it difficult or impossible to draw valid conclusions about the effect of each factor.
1
Determine whether or not the following samples are representative. If they are not, write the reasons.

1. To find the average GPA of all students in a university, use all honor students at the university as the sample.
_______
2. To find out the most popular cereal among young people under the age of ten, stand outside a large supermarket for three hours and speak to every twentieth child under age ten who enters the supermarket.
_______

3. To find the average annual income of all adults in the United States, sample U.S. Representatives. Create a cluster sample by considering each state as a stratum (group). By using simple random sampling, select states to be part of the cluster. Then survey every U.S. Representative in the cluster.
_______

4. To determine the proportion of people taking public transportation to work, survey 20 people in New York City. Conduct the survey by sitting in Central Park on a bench and interviewing every person who sits next to you.
_______

5. To determine the average cost of a two-day stay in a hospital in Massachusetts, survey 100 hospitals across the state using simple random sampling.
_______
Examples
1
Determine what is the type of sampling in each case

  1. A sample of 100 undergraduate San Jose State students is taken by organizing the students’ names by classification (first-year, sophomore, junior, or senior), and then selecting 25 students from each.__________
  2. A random number generator is used to select a student from the alphabetical listing of all undergraduate students in the Fall semester. Starting with that student, every 50th student is chosen until 75 students are included in the sample.__________
  3. A completely random method is used to select 75 students. Each undergraduate student in the fall semester has the same probability of being chosen at any stage of the sampling process. __________
  4. The first-year, sophomore, junior, and senior years are numbered one, two, three, and four, respectively. A random number generator is used to pick two of those years. All students in those two years are in the sample. __________
  5. An administrative assistant is asked to stand in front of the library one Wednesday and to ask the first 100 undergraduate students he encounters what they paid for tuition the Fall semester. Those 100 students are the sample. __________
  6. A soccer coach selects six players from a group of boys aged eight to ten, seven players from a group of boys aged 11 to 12, and three players from a group of boys aged 13 to 14 to form a recreational soccer team. __________
  7. A pollster interviews all human resource personnel in five different high tech companies. __________
  8. A high school educational researcher interviews 50 public high school teachers and 50 private high school teachers. __________
  9. A medical researcher interviews every third cancer patient from a list of cancer patients at a local hospital. __________
  10. A high school counselor uses a computer to generate 50 random numbers and then picks students whose names correspond to the numbers. __________
  11. A student interviews classmates in their algebra class to determine how many pairs of jeans a student owns, on the average. __________
Sample Size
In Confidence Intervals of the text, sample size formulas are provided which will determine sample sizes when sampling from a population. The sample size will be a function of the desired precision and not a function of the population size. It may be somewhat counterintuitive that the sample size does not depend on the population size. However, this implies that a sample size of 1,000 can be adequate to represent a population of 100,000 versus 1,000,000 given that the same level of precision is desired. When working in Confidence Intervals with sample size formulas, the student will notice that population size is not a factor in determining the sample size.
Suppose ABC College has 10,000 part-time students (the population). We are interested in the average amount of money a part-time student spends on books in the fall term. Asking all 10,000 students is an almost impossible task.
Suppose we take two different samples.

First, we use convenience sampling and survey ten students from a first term organic chemistry class. Many of these students are taking first term calculus in addition to the organic chemistry class. The amount of money they spend on books is as follows:
$128; $87; $173; $116; $130; $204; $147; $189; $93; $153

The second sample is taken using a list of senior citizens who take P.E. classes and taking every fifth senior citizen on the list, for a total of ten senior citizens. They spend:
$50; $40; $36; $15; $50; $100; $40; $53; $22; $22

It is unlikely that any student is in both samples.
1

Do you think that either of these samples is representative of (or is characteristic of) the entire 10,000 part-time student population?

1

Since these samples are not representative of the entire population, is it wise to use the results to describe the entire population?

1

Now, suppose we take a third sample. We choose ten different part-time students from the disciplines of chemistry, math, English, psychology, sociology, history, nursing, physical education, art, and early childhood development. (We assume that these are the only disciplines in which part-time students at ABC College are enrolled and that an equal number of part-time students are enrolled in each of the disciplines.) Each student is chosen using simple random sampling. Using a calculator, random numbers are generated and a student from a particular discipline is selected if they have a corresponding number. The students spend the following amounts:
$180; $50; $150; $85; $260; $75; $180; $200; $200; $150


Is the sample biased?

A local radio station has a fan base of 20,000 listeners. The station wants to know if its audience would prefer more music or more talk shows. Asking all 20,000 listeners is an almost impossible task.

The station uses convenience sampling and surveys the first 200 people they meet at one of the station’s music concert events. 24 people said they’d prefer more talk shows, and 176 people said they’d prefer more music.
1

Do you think that this sample is representative of (or is characteristic of) the entire 20,000 listener population?

1

What do you recommend they do to make their study unbiased?

Variation

Variation in Data


Variation is present in any set of data. For example, 16-ounce cans of beverage may contain more or less than 16 ounces of liquid. In one study, eight 16-ounce cans were measured and produced the following amount (in ounces) of beverage:
15.8; 16.1; 15.2; 14.8; 15.8; 15.9; 16.0; 15.5

Variation in Samples

Two samples taken from the population will likely be different from each other, although they may be close. The larger the sample size, the closer the data will be to each other. This is variability in samples.

Size of Sample

Samples thus far have been small. Usually polling samples of 1,200 and 1,500 is considered big enough if done random. Be aware that convince sampling and call in surveys will still create biased.
1
Divide into groups of two, three, or four. Your instructor will give each group one six-sided die. Try this experiment twice. Roll one fair die (six-sided) 20 times. Record the number of ones, twos, threes, fours, fives, and sixes you

First 20 rolls
1s _______
2s_______
3s_______
4s_______
5s_______
6s_______
1
Divide into groups of two, three, or four. Your instructor will give each group one six-sided die. Try this experiment twice. Roll one fair die (six-sided) 20 times. Record the number of ones, twos, threes, fours, fives, and sixes you

2nd 20 rolls
1s _______
2s_______
3s_______
4s_______
5s_______
6s_______
Homework
Classwork 53-79 odd

https://openstax.org/books/introductory-statistics-2e/pages/1-homework
1

Input homework here