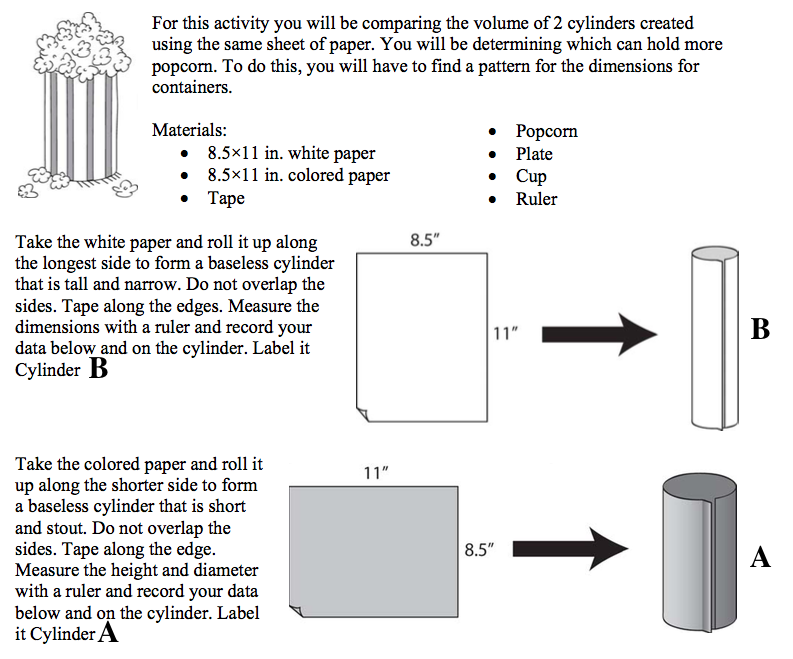
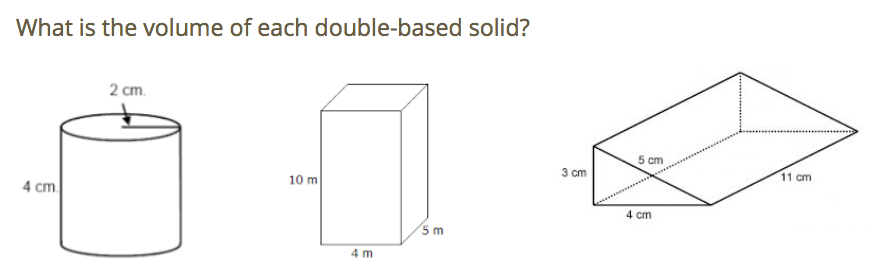
Investigating Volume of Cylinders

By David Kwan

Last updated over 6 years ago

27 Questions

Note from the author:

This Formative is by: Rebecca Mann

This is an activity introducing volume in a high school geometry class.  Using a 3-Act Math Task and an Illuminations Task, students conceptualize the idea of volume and develop the volume of cylinders.   

Watch the Act 1:  Popcorn Picker Video Below.

Based on the video, what question(s) could we explore?

Which container will hold more popcorn?

What information do you need to explore the question?

Act 2: POPCORN CYLINDER TASK

Do you think the two cylinders will hold the same amount? Do you think one will hold more than the other one? Which one? Why?

Come get your popcorn when everyone in your group has completed everything up to this point.

***Read Carefully!!! Place Cylinder A on the paper plate with Cylinder B inside it.  Use your cup to pour popcorn into Cylinder B until it is full.  Carefully, lift Cylinder B so that the popcorn falls into Cylinder A.

Describe what happened. Is Cylinder A full, not full, or overflowing?

As you share your popcorn snack, answer the following questions.  

Was your prediction correct? How do you know?

If your prediction was incorrect, describe what actually happened.

Act 3: Popcorn Picker Solution

Can a rectangular piece of paper give you the same amount of popcorn no matter how you make the cylinder?

Watch the video below to see if your prediction is correct. 

Deriving the Volume of a Cylinder
Move the slider to see how the cylinder is being filled on the GeoGebra applet below.  

The applet above illustrates how the cylinder is being filled to specific heights. We can think of volume of a cylinder as stacking ____________________ to a specific height.

Calculate the volume of Cylinder A. Label your dimensions on the diagram.

Calculate the volume of Cylinder B. Label your dimensions on the diagram.

Explain why the cylinders do or do not hold the same amount of popcorn. Use the formula for the volume of a cylinder to guide your explanation.

Which measurement impacts the volume of more: the radius or the height?

Why do you believe your response to #19 is true?

By how much would you have to decrease the height of the Cylinder A to make the volumes of the two cylinders equal?

Cavalieri's Principle - GeoGebra Applet

Click the play button to begin the applet.  

Why do the two solids contain the same amount of volume?

Check the box beside "Solids" on the applet.  

What do you notice?

This applet visually describes the Cavalieri's Principle. Based on what you have observed, what is Cavalieri's Principle in your own words?

CLOSER - BY YOURSELF. :)