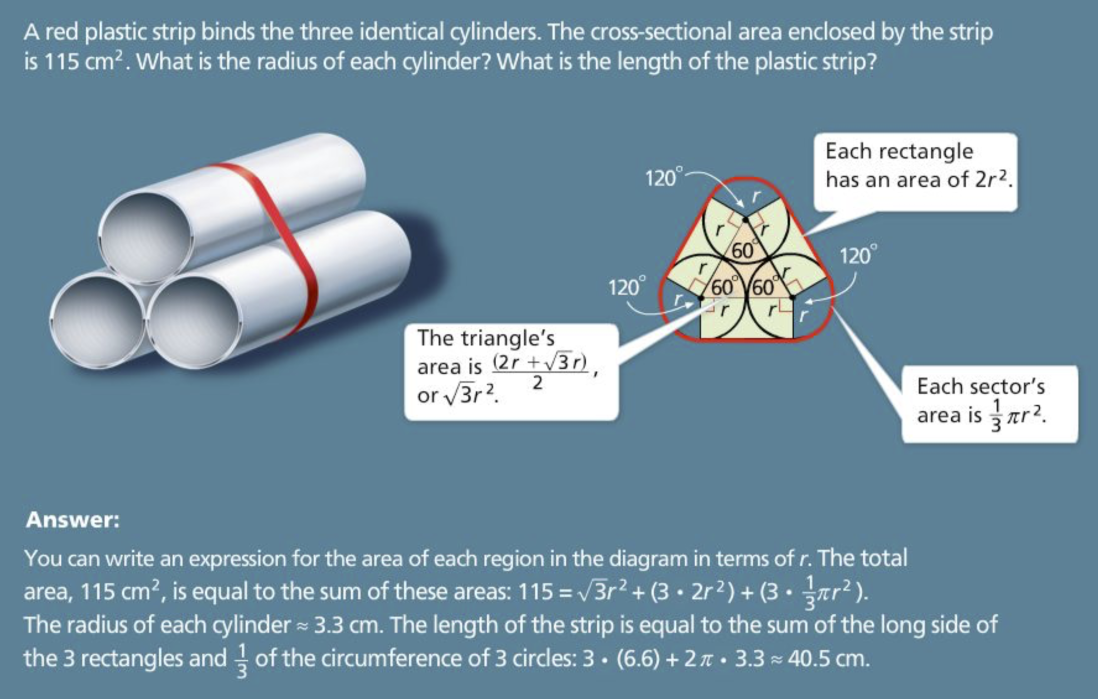
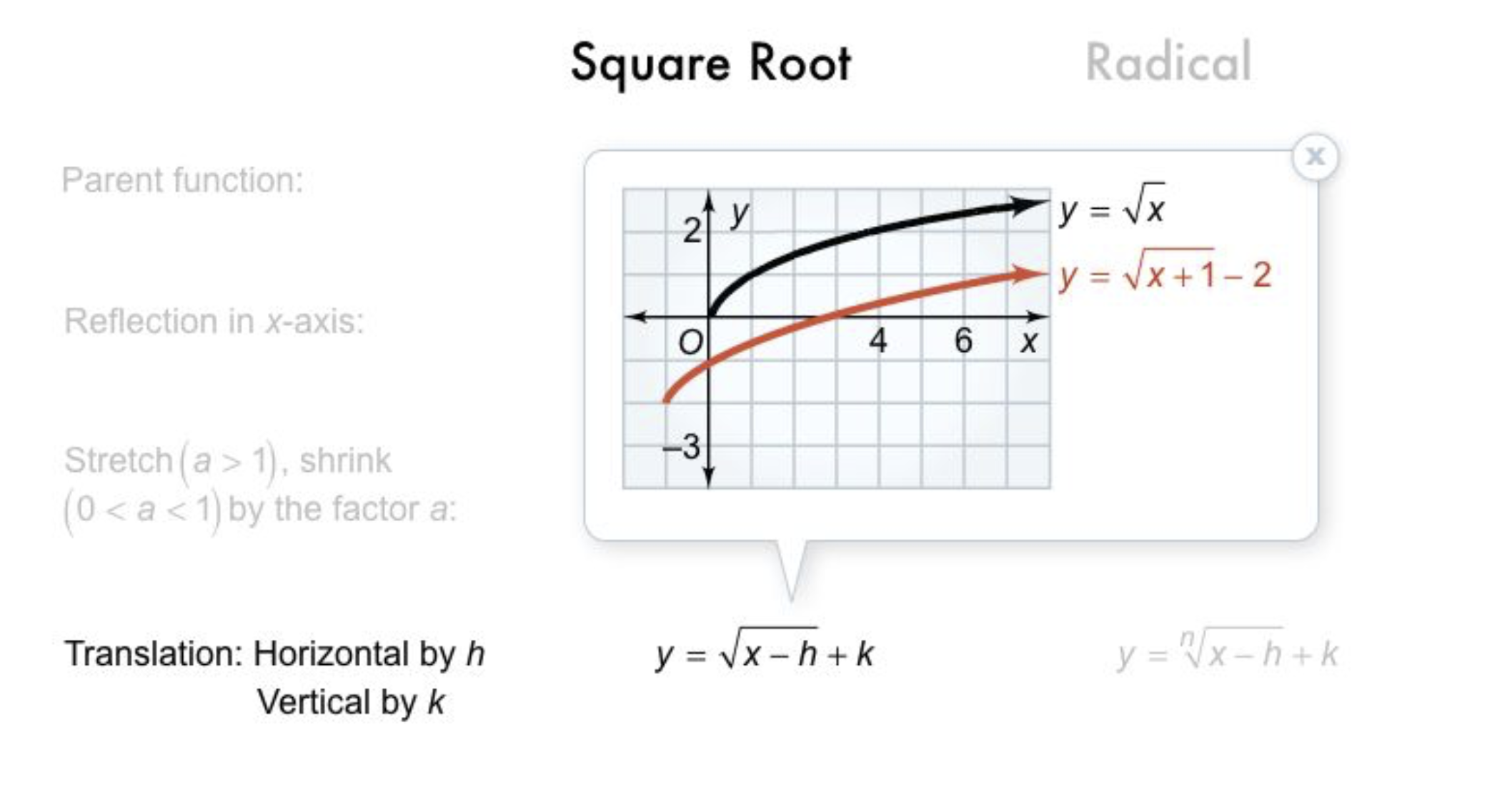
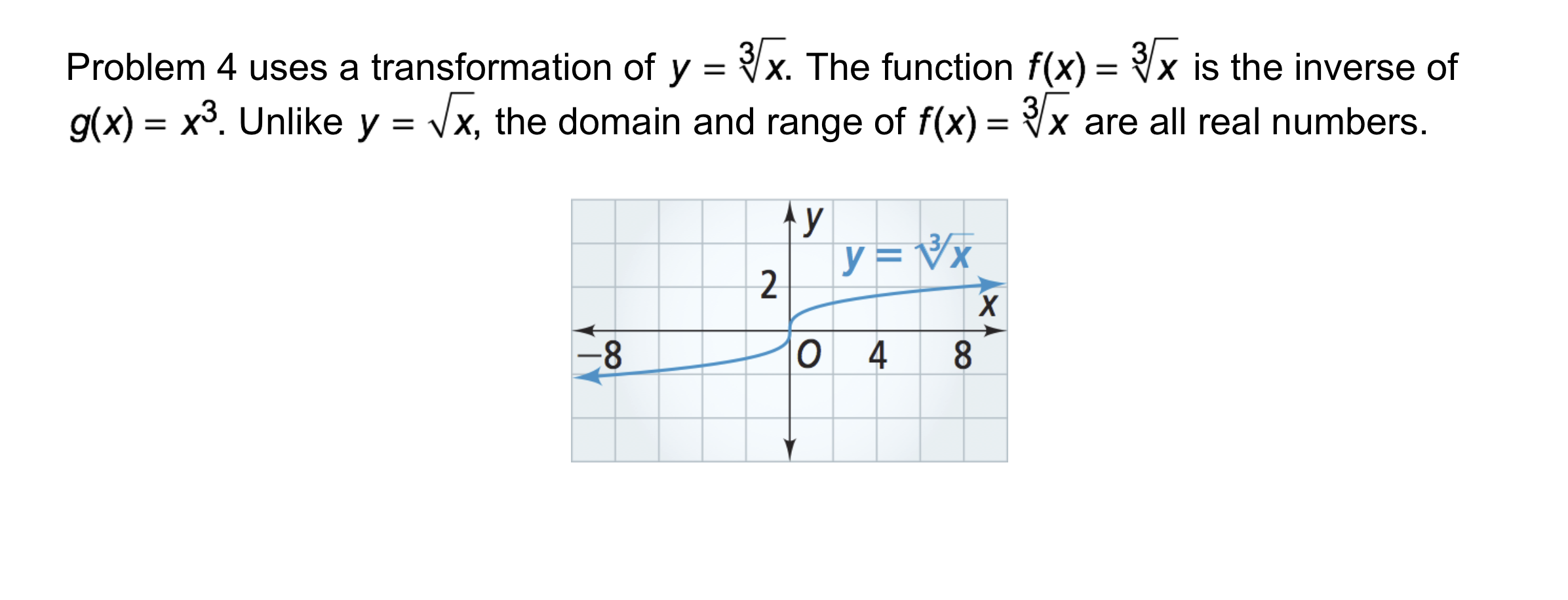
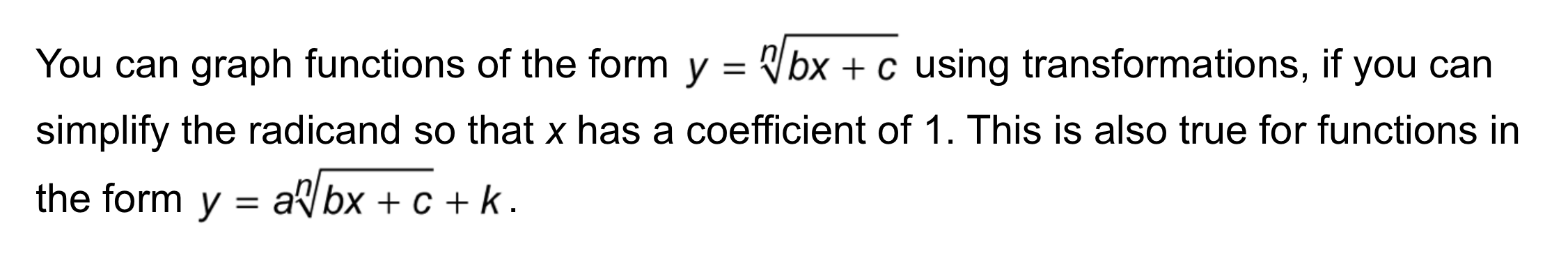Algebra 2 6-8 Complete Lesson: Graphing Radical Functions
star
star
star
star
star
Last updated about 4 years ago
25 questions
Note from the author:
10
F.IF.7.b
10
F.IF.7.b
10
F.IF.7.b
10
F.IF.7.b
10
F.IF.7.b
10
F.IF.7.b
30
F.IF.7.b
30
F.IF.7.b
10
F.IF.7.b
10
F.IF.7.b
10
F.BF.4.a
10
N.RN.2
10
A.REI.4.b
30
A.REI.4.b
30
A.REI.4.b
5
5
5
10
G.CO.2
10
100
10
F.IF.7.b